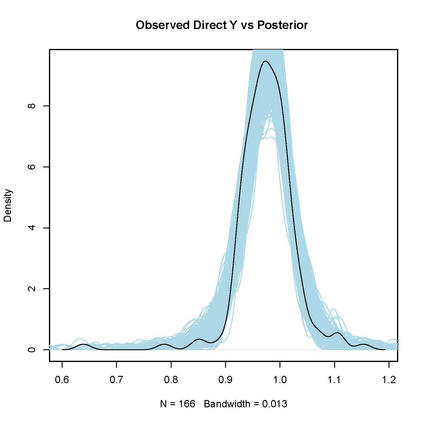
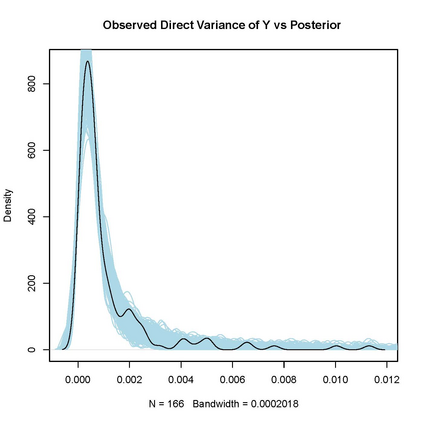
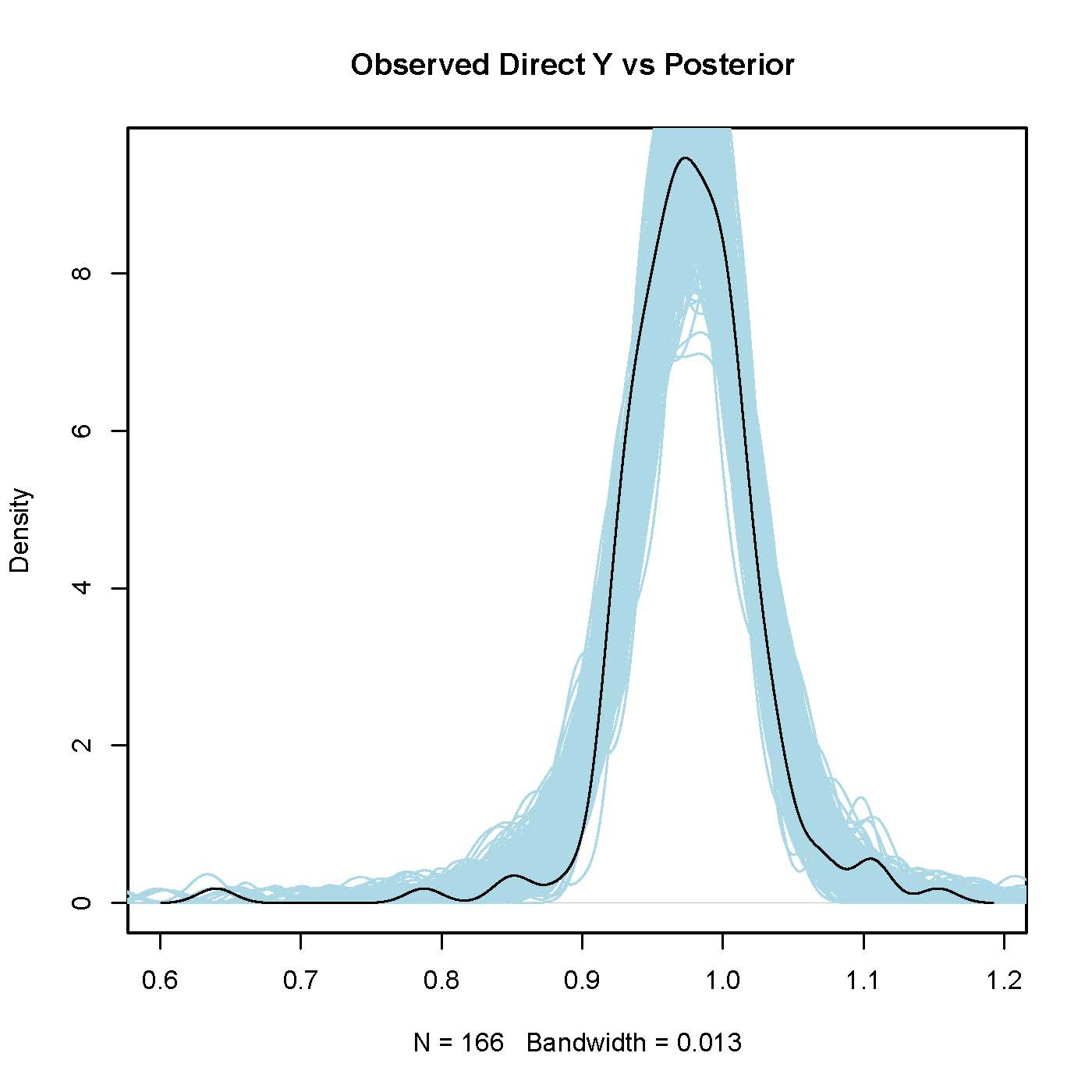
The mean field variational Bayes (VB) algorithm implemented in Stan is relatively fast and efficient, making it feasible to produce model-estimated official statistics on a rapid timeline. Yet, while consistent point estimates of parameters are achieved for continuous data models, the mean field approximation often produces inaccurate uncertainty quantification to the extent that parameters are correlated a posteriori. In this paper, we propose a simulation procedure that calibrates uncertainty intervals for model parameters estimated under approximate algorithms to achieve nominal coverages. Our procedure detects and corrects biased estimation of both first and second moments of approximate marginal posterior distributions induced by any estimation algorithm that produces consistent first moments under specification of the correct model. The method generates replicate datasets using parameters estimated in an initial model run. The model is subsequently re-estimated on each replicate dataset, and we use the empirical distribution over the re-samples to formulate calibrated confidence intervals of parameter estimates of the initial model run that are guaranteed to asymptotically achieve nominal coverage. We demonstrate the performance of our procedure in Monte Carlo simulation study and apply it to real data from the Current Employment Statistics survey.
翻译:暂无翻译