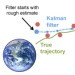
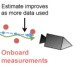
We study a class of Gaussian processes for which the posterior mean, for a particular choice of data, replicates a truncated Taylor expansion of any order. The data consists of derivative evaluations at the expansion point and the prior covariance kernel belongs to the class of Taylor kernels, which can be written in a certain power series form. This permits statistical modelling of the uncertainty in a variety of algorithms that exploit first and second order Taylor expansions. To demonstrate the utility of this Gaussian process model we introduce new probabilistic versions of the classical extended Kalman filter for non-linear state estimation and the Euler method for solving ordinary differential equations.
翻译:我们研究的Gaussian程序类别,其后继法意味着,对于特定的数据选择来说,其后继法是复制一个短短的泰勒扩展顺序。数据包括扩张点的衍生评价,先前的共变量内核属于泰勒内核的类别,可以以某种权力序列的形式写成。这样就可以对利用泰勒扩展的第一和第二顺序的各种算法的不确定性进行统计建模。为了证明这个高森进程模式的效用,我们引入了用于非线性国家估算的古典卡曼扩展过滤器的新的概率性版本,以及解决普通差异方程式的尤勒法。