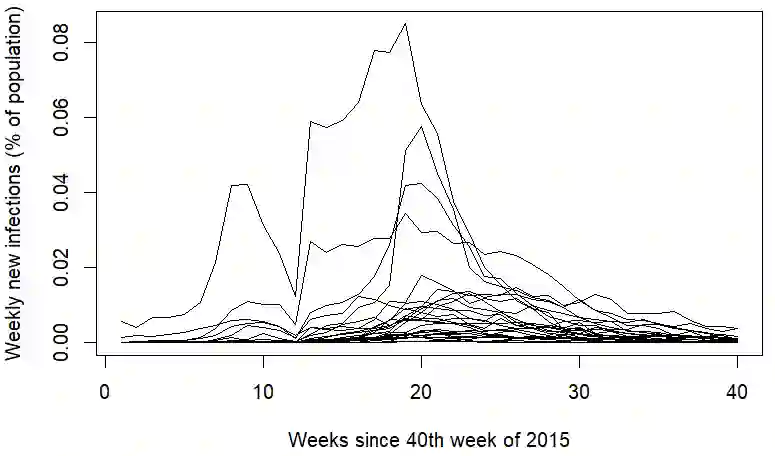
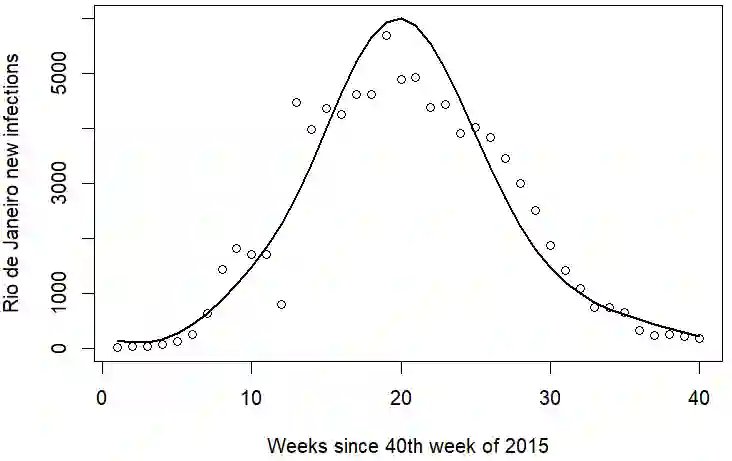
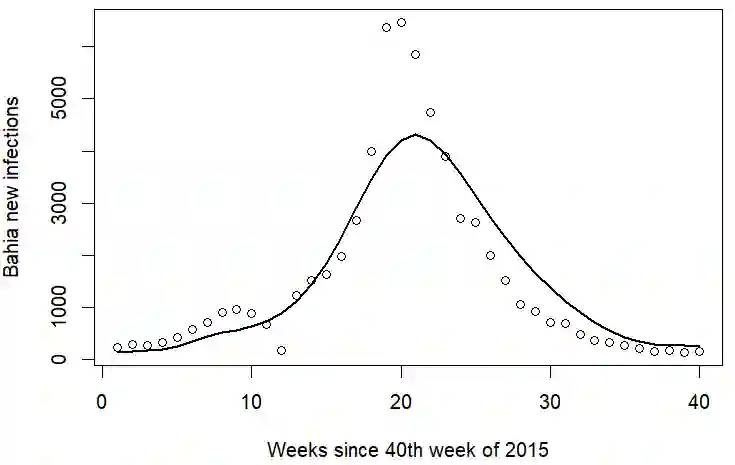
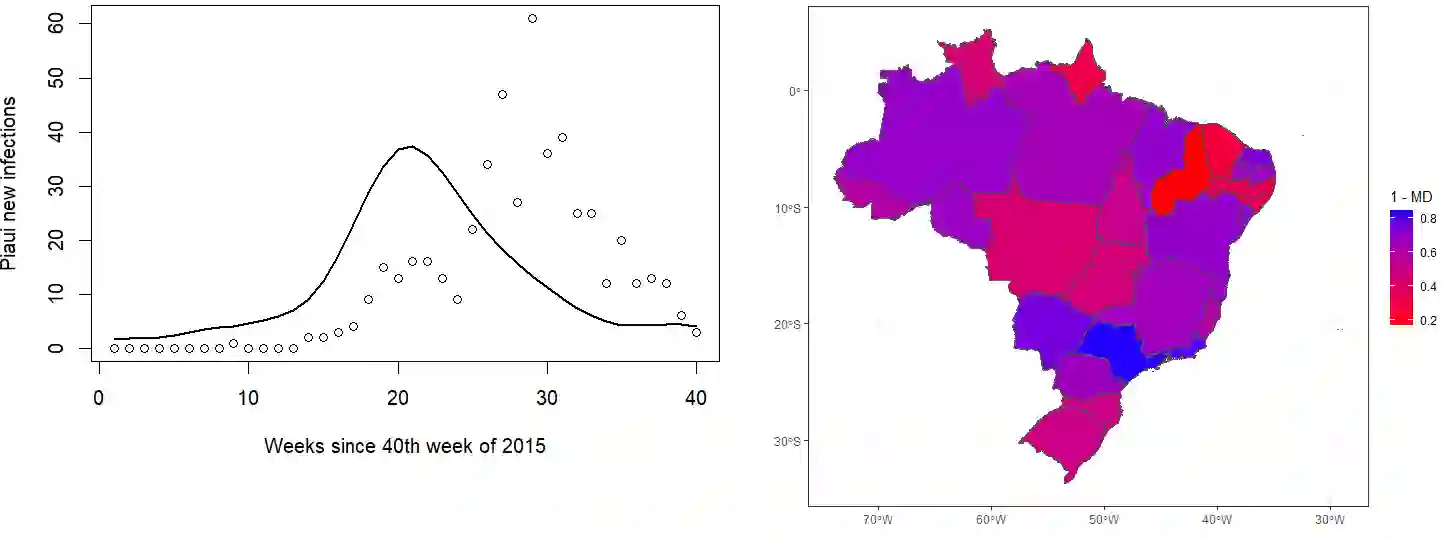
The dynamics that govern disease spread are hard to model because infections are functions of both the underlying pathogen as well as human or animal behavior. This challenge is increased when modeling how diseases spread between different spatial locations. Many proposed spatial epidemiological models require trade-offs to fit, either by abstracting away theoretical spread dynamics, fitting a deterministic model, or by requiring large computational resources for many simulations. We propose an approach that approximates the complex spatial spread dynamics with a Gaussian process. We first propose a flexible spatial extension to the well-known SIR stochastic process, and then we derive a moment-closure approximation to this stochastic process. This moment-closure approximation yields ordinary differential equations for the evolution of the means and covariances of the susceptibles and infectious through time. Because these ODEs are a bottleneck to fitting our model by MCMC, we approximate them using a low-rank emulator. This approximation serves as the basis for our hierarchical model for noisy, underreported counts of new infections by spatial location and time. We demonstrate using our model to conduct inference on simulated infections from the underlying, true spatial SIR jump process. We then apply our method to model counts of new Zika infections in Brazil from late 2015 through early 2016.
翻译:控制疾病传播的动态很难建模, 因为感染既是病原体的功能,也是人类或动物行为的功能。 当模拟不同空间地点之间疾病传播的方式时,这个挑战就更加艰巨。 许多拟议的空间流行病学模型需要权衡,以便通过抽取理论扩散动态、安装确定性模型或需要大量计算资源来适应许多模拟。 我们提出一种方法,用高斯过程来比较复杂的空间分布动态。 我们首先提议将空间空间分布动态与众所周知的SIR随机过程相近,然后我们为这个随机过程得出一个短暂的近似。 这个瞬间近似将产生普通的差别方程式, 用于改变易感性和传染性的手段和共变异性, 并随着时间的推移。 由于这些计算模型对于由MCC的模型来适应我们的模型, 我们用低级别模拟器来比较这些模型。 这个近似可以作为我们按空间位置和时间对新感染进行低级别统计的基础, 然后我们用模型来模拟我们从2015年期到2015年年期的SIR系统系统系统系统 的快速测试到2015年期空间感染测测测序。