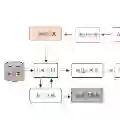
Entity resolution (ER), comprising record linkage and de-duplication, is the process of merging noisy databases in the absence of unique identifiers to remove duplicate entities. One major challenge of analysis with linked data is identifying a representative record among determined matches to pass to an inferential or predictive task, referred to as the \emph{downstream task}. Additionally, incorporating uncertainty from ER in the downstream task is critical to ensure proper inference. To bridge the gap between ER and the downstream task in an analysis pipeline, we propose five methods to choose a representative (or canonical) record from linked data, referred to as canonicalization. Our methods are scalable in the number of records, appropriate in general data scenarios, and provide natural error propagation via a Bayesian canonicalization stage. The proposed methodology is evaluated on three simulated data sets and one application -- determining the relationship between demographic information and party affiliation in voter registration data from the North Carolina State Board of Elections. We first perform Bayesian ER and evaluate our proposed methods for canonicalization before considering the downstream tasks of linear and logistic regression. Bayesian canonicalization methods are empirically shown to improve downstream inference in both settings through prediction and coverage.
翻译:实体分辨率(ER)由记录链接和减少重复组成,是一个在缺乏独特的识别特征的情况下将噪音数据库合并的过程,以清除重复的实体。对链接数据进行分析的一个主要挑战是如何在确定匹配对象之间找到一种具有代表性的记录,以便传递给称为\emph{downstream任务的推断或预测任务。此外,在下游任务中纳入ER的不确定性对于确保正确推断至关重要。为了缩小ER与分析管道中下游任务之间的差距,我们建议了从链接数据中选择一种代表(或直通)记录(或直通)记录(称为Canonicalization)的五种方法,即从链接数据中选择一种代表(或直通)记录,称为Canonicalization。我们的方法在一般数据假设情况下可以扩缩记录的数量,并通过Bayesian Chanicolicization 阶段提供自然错误传播。拟议方法在三个模拟数据集和一个应用程序上进行了评价 -- -- 确定人口信息与北卡罗来纳州选举委员会选民登记数据中的党派关系。我们首先执行Bayesian ER,在考虑线性和后勤回归的下游任务之前评估我们提出的罐化方法。Bayesian survicurviviculviviewsurviewsurvidududududududududududududustration 方法。