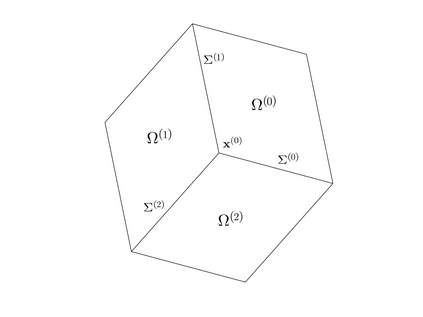
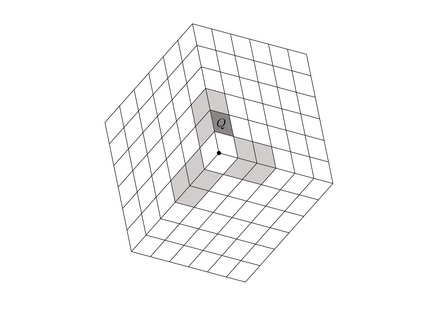
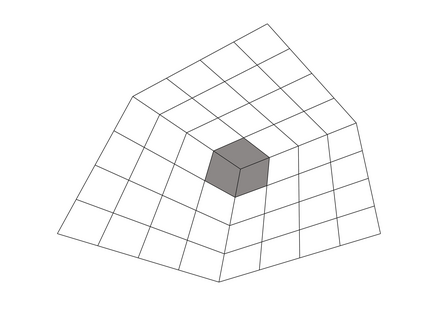
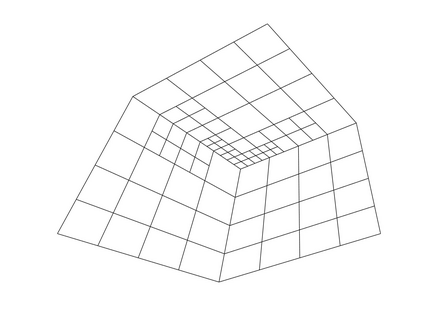
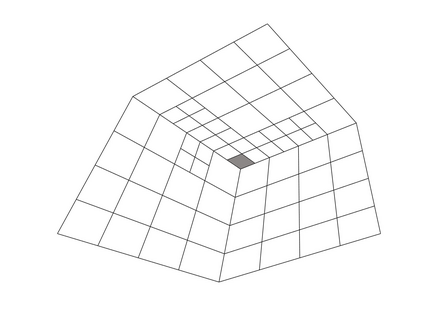
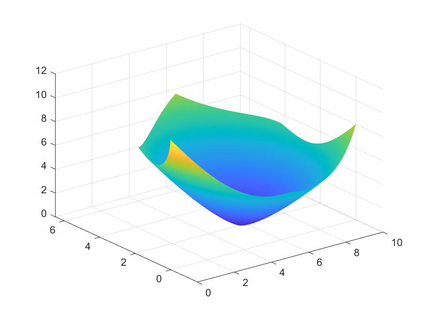
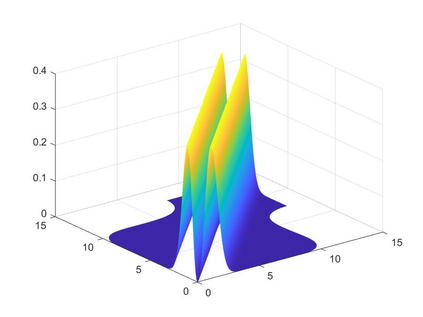
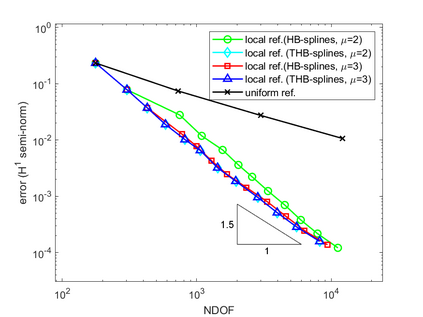
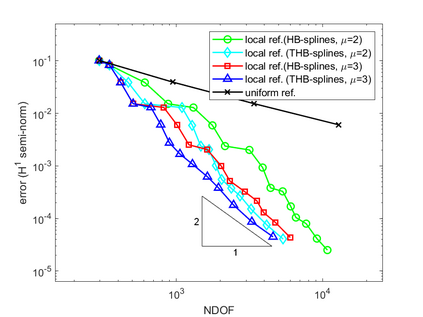
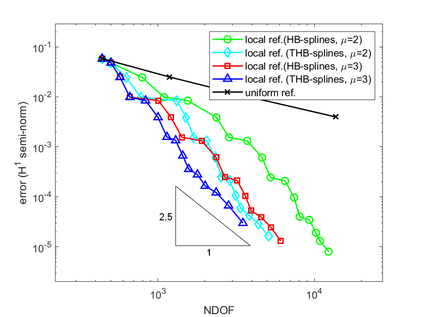
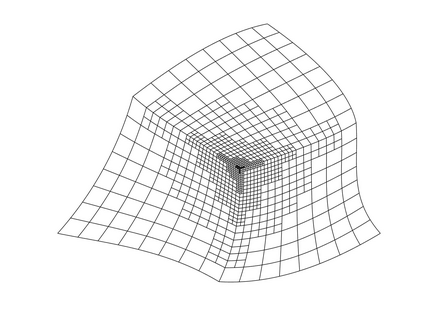
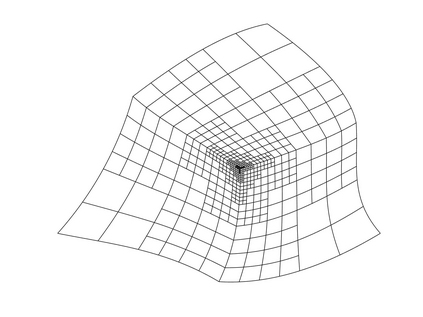
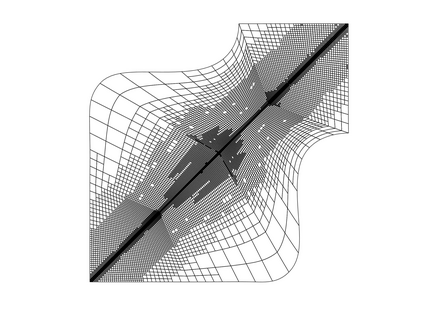
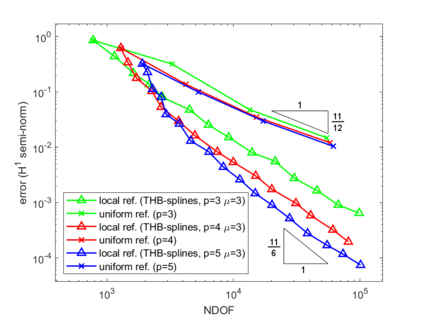
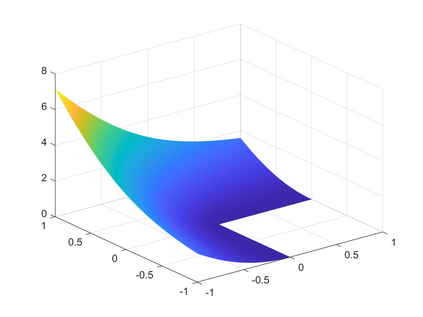
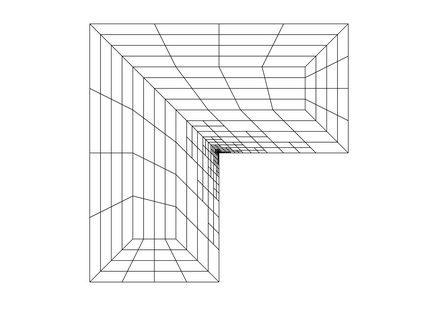
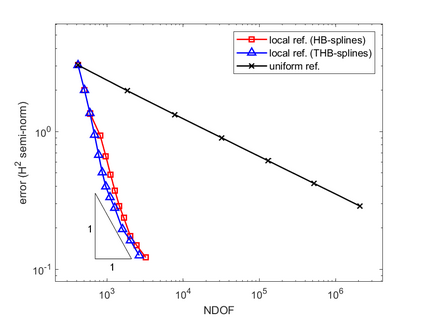
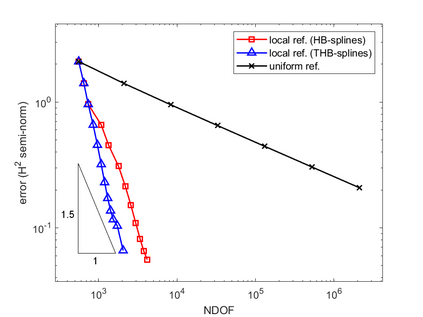
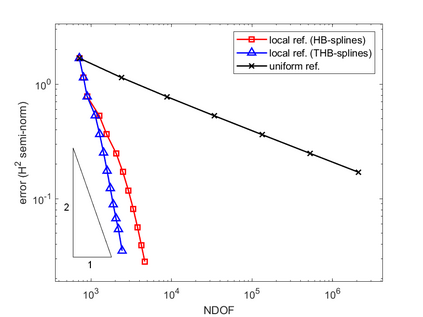
Isogeometric analysis is a powerful paradigm which exploits the high smoothness of splines for the numerical solution of high order partial differential equations. However, the tensor-product structure of standard multivariate B-spline models is not well suited for the representation of complex geometries, and to maintain high continuity on general domains special constructions on multi-patch geometries must be used. In this paper we focus on adaptive isogeometric methods with hierarchical splines, and extend the construction of $C^1$ isogeometric spline spaces on multi-patch planar domains to the hierarchical setting. We introduce a new abstract framework for the definition of hierarchical splines, which replaces the hypothesis of local linear independence for the basis of each level by a weaker assumption. We also develop a refinement algorithm that guarantees that the assumption is fulfilled by $C^1$ splines on certain suitably graded hierarchical multi-patch mesh configurations, and prove that it has linear complexity. The performance of the adaptive method is tested by solving the Poisson and the biharmonic problems.
翻译:Isogoricat 分析是一种强大的范例,它利用高顺序部分差异方程式数字解决方案的高平稳性样板。然而,标准多变B-spline模型的抗拉产品结构并不非常适合代表复杂的几何,而且为了在一般领域保持高度连续性,必须使用多端地理图案的特殊构造。在本文中,我们侧重于使用高等级样板的适应性等离子测量方法,并将多级平板域的1美元等离子测量样板空间的构造扩大到等级设置。我们为等级样板定义引入了新的抽象框架,以较弱的假设取代了每个级别基础的当地线性独立假设。我们还制定了一种精细的算法,保证在某些合适的等级等级等级的多级图案集图案配置上用1美元来完成这一假设,并证明它具有线性复杂性。适应方法的性能通过解决Poisson和双调问题来测试。