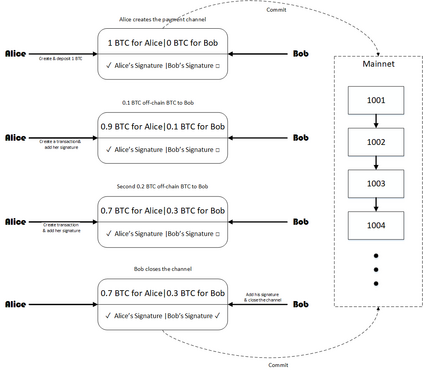
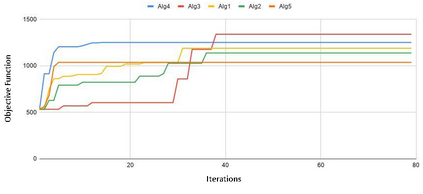
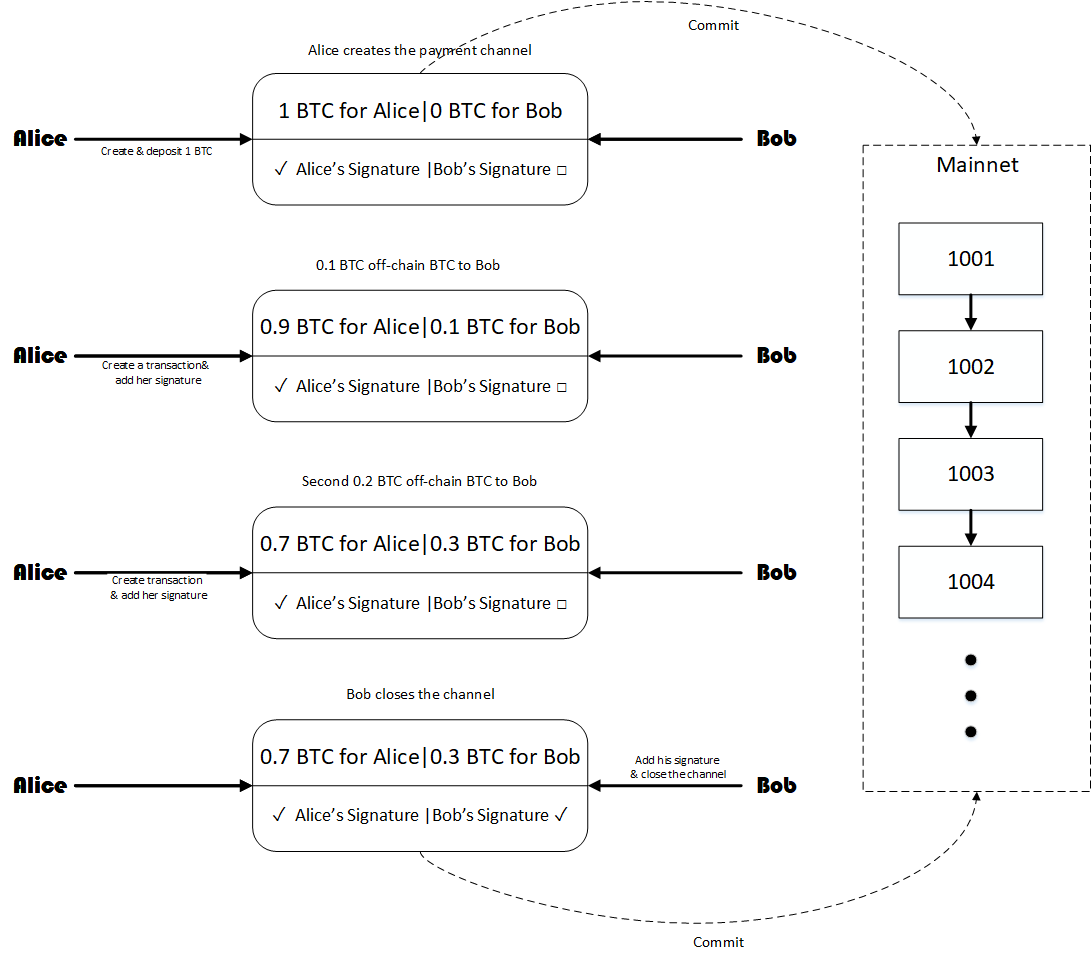
Payment channel is a protocol which allows cryptocurrency users to route multiple transactions through network without committing them to the main blockchain network (mainnet). This ability makes them the most prominent solution to blockchains' scalability problem. Each modification of payment channels requires a transaction on the mainnet and therefore, big transaction fees. In this paper, we assume that a set of payment transactions are given (batch or online) and we study the problem of scheduling modificiations on payment channels to route all of the transactions with minimum modification cost. We investigate two cost models for aforementioned problem: the step cost function in which every channel modification has a constant cost and the linear cost function in which modification costs are proportional to the amount of change. For the step cost function model, we prove impossibility results for both batch and online case. Moreover, some heuristic methods for the batch case are presented and compared. For the linear cost we propose a polynomial time algorithm using linear programming for the batch case.
翻译:支付渠道是一种协议,允许加密货币用户在不将其投入主链链网络(manet)的情况下通过网络进行多种交易。 这种能力使他们成为块链可缩缩问题的最突出解决办法。 每次修改支付渠道都要求在主网上进行交易,因此是大额交易费。 在本文中,我们假定提供了一套付款交易(批量或在线),我们研究支付渠道上安排调整以最低修改成本处理所有交易的问题。我们调查了上述问题的两个成本模型:每个频道修改都具有固定成本的职级成本函数和调整成本与变化量成比例的线性成本函数。对于职档成本模型,我们证明批量和在线案例都不可能产生结果。此外,还提出并比较了批量案件的一些超常方法。对于线性成本,我们建议使用批量案例线性编程的多元时间算法。