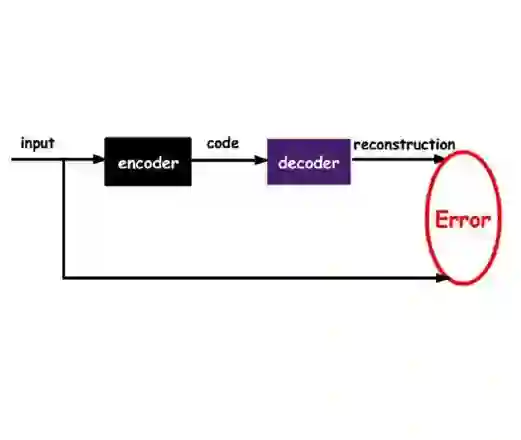
Projection-based model order reduction on nonlinear manifolds has been recently proposed for problems with slowly decaying Kolmogorov n-width such as advection-dominated ones. These methods often use neural networks for manifold learning and showcase improved accuracy over traditional linear subspace-reduced order models. A disadvantage of the previously proposed methods is the potential high computational costs of training the networks on high-fidelity solution snapshots. In this work, we propose and analyze a novel method that overcomes this disadvantage by training a neural network only on subsampled versions of the high-fidelity solution snapshots. This method coupled with collocation-based hyper-reduction and Gappy-POD allows for efficient and accurate surrogate models. We demonstrate the validity of our approach on a 2d Burgers problem.
翻译:摘要:最近针对在Kolmogorov n-width缓慢下降的问题,如以对流为主的问题,提出了基于投影的非线性流形模型降阶。这些方法通常使用神经网络进行流形学习,并展示了相对于传统线性替代模型的优越性。以前提出的方法的一个缺点是在高保真解快照上训练网络时可能会产生高计算成本。在这项工作中,我们提出和分析了一种新方法,通过仅在高保真解快照的子抽样版本上训练神经网络来克服这个缺点。这种方法结合基于配点的超体积简化和Gappy-POD,可以提供高效准确的代理模型。我们在一个二维Burgers问题上证明了我们的方法的有效性。