Uncertainty quantification for fault slip inversion

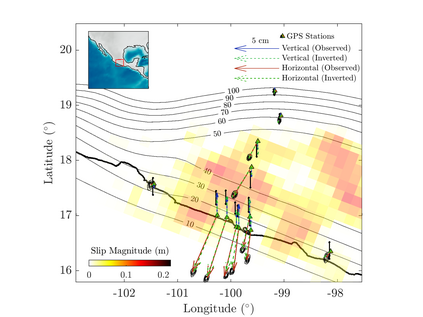
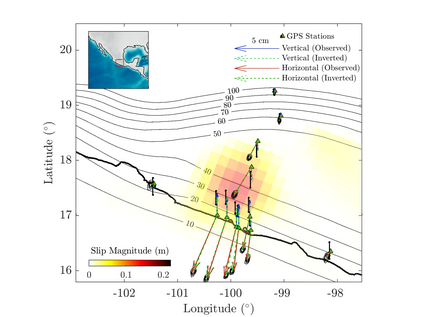
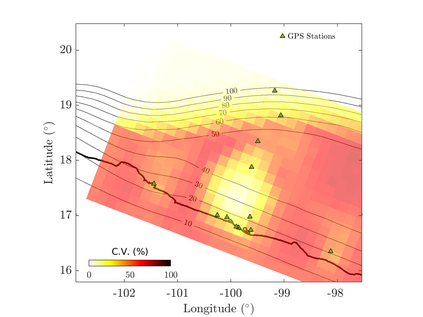
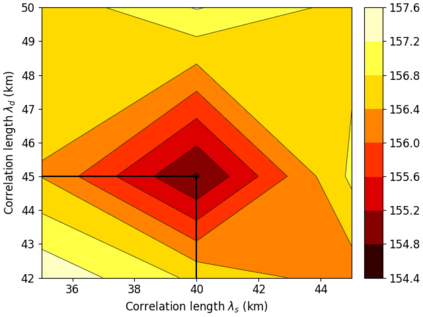
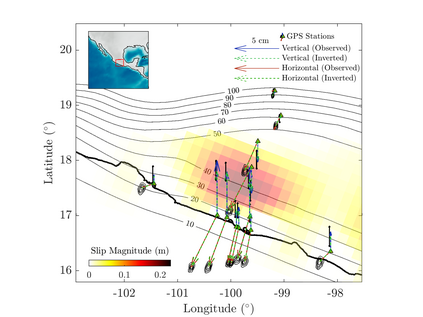
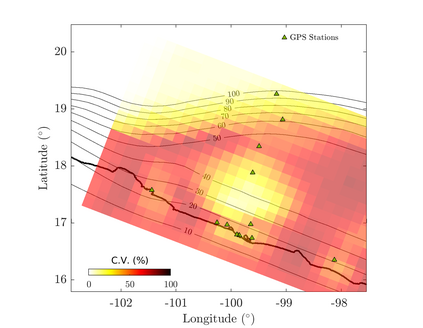
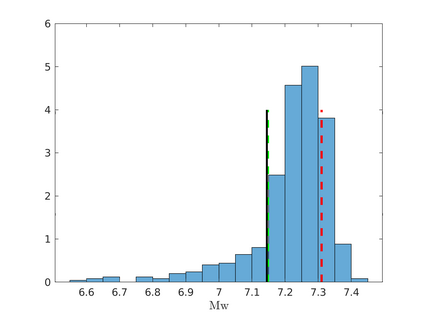
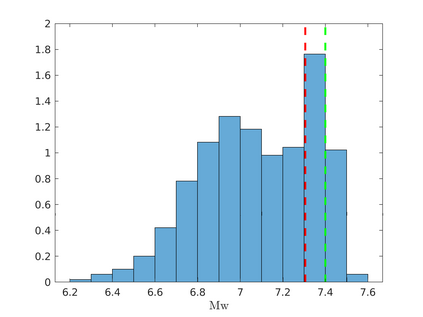
We propose an efficient Bayesian approach to infer a fault displacement from geodetic data in a slow slip event. Our physical model of the slip process reduces to a multiple linear regression subject to constraints. Assuming a Gaussian model for the geodetic data and considering a truncated multivariate normal prior distribution for the unknown fault slip, the resulting posterior distribution is also truncated multivariate normal. Regarding the posterior, we propose an algorithm based on Optimal Directional Gibbs that allows us to efficiently sample from the resulting high-dimensional posterior distribution of along dip and along strike movements of our fault grid division. A synthetic fault slip example illustrates the flexibility and accuracy of the proposed approach. The methodology is also applied to a real data set, for the 2006 Guerrero, Mexico, Slow Slip Event, where the objective is to recover the fault slip on a known interface that produces displacements observed at ground geodetic stations. As a by-product of our approach, we are able to estimate moment magnitude for the 2006 Guerrero Event with uncertainty quantification.