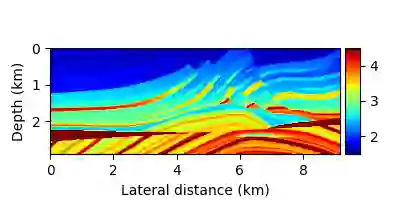
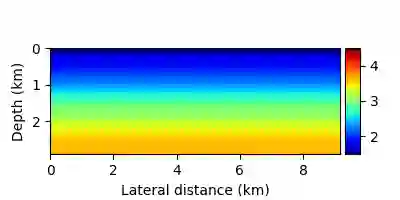
PDE-constrained optimization problems are often treated using the reduced formulation where the PDE constraints are eliminated. This approach is known to be more computationally feasible than other alternatives at large scales. However, the elimination of the constraints forces the optimization process to fulfill the constraints at all times. In some problems this may lead to a highly non-linear objective, which is hard to solve. An example to such a problem, which we focus on in this work, is Full Waveform Inversion (FWI), which appears in seismic exploration of oil and gas reservoirs, and medical imaging. In an attempt to relieve the non-linearity of FWI, several approaches suggested to expand the optimization search space and relax the PDE constraints. This comes, however, with severe memory and computational costs, which we aim to reduce. In this work we adopt the expanded search space approach, and suggest a new formulation of FWI using extended source functions. To make the source-extended problem more feasible in memory and computations, we couple the source extensions in the form of a low-rank matrix. This way, we have a large-but-manageable additional parameter space, which has a rather low memory footprint, and is much more suitable for solving large scale instances of the problem than the full rank additional space. In addition, we show how our source-extended approach is applied together with the popular simultaneous sources technique -- a stochastic optimization technique that significantly reduces the computations needed for FWI inversions. We demonstrate our approaches for solving FWI problems using 2D and 3D models with high frequency data only.
翻译:受PDE限制的优化问题往往在消除PDE限制因素的减少配方中加以处理。这一方法在计算上比其他大规模替代方法更加可行。然而,消除限制迫使优化过程在任何时候都满足限制。在有些问题上,这可能导致高度非线性目标,很难解决。我们在此工作中重点研究的一个问题的例子就是全波转换(FWI),它出现在石油和天然气储油库地震勘探和医疗成像中。为了缓解FWI的非线性,我们建议采取几种方法扩大优化搜索空间,并放松PDE限制。然而,随着严格的记忆和计算成本的减少,我们的目标是减少这些限制。在这项工作中,我们采用扩大搜索空间方法,并提出使用扩展源功能功能的新方案。为了在记忆和计算中更加可行,我们仅将源性扩展模式与低级矩阵形式相匹配。这样,我们有一个大但可操作的额外参数空间定位空间应用空间应用空间应用空间应用率非常低,而我们又要大量使用高的缩缩略图。