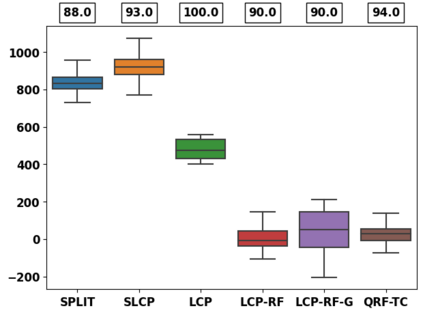
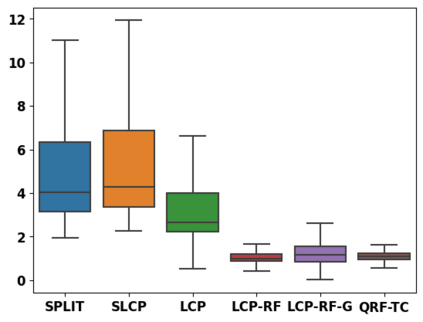
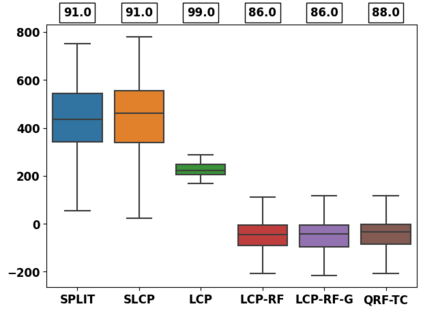
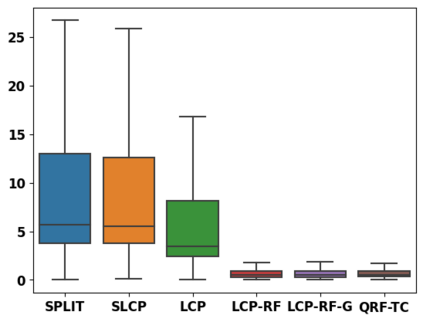
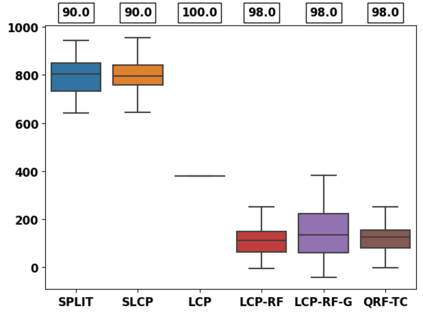
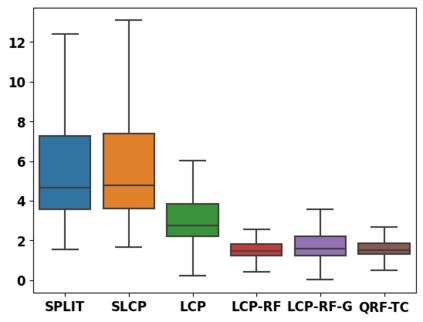
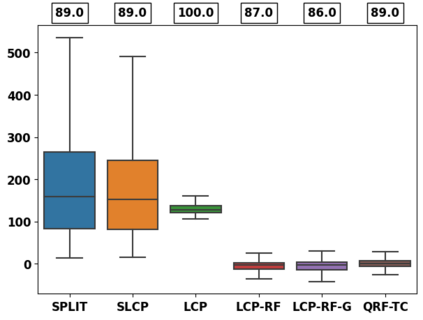
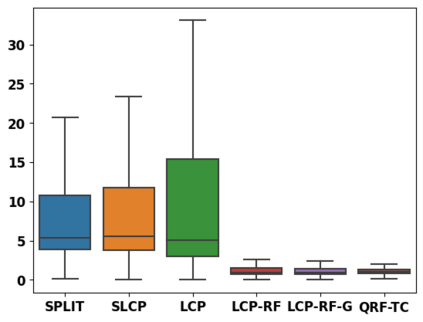
Despite attractive theoretical guarantees and practical successes, Predictive Interval (PI) given by Conformal Prediction (CP) may not reflect the uncertainty of a given model. This limitation arises from CP methods using a constant correction for all test points, disregarding their individual uncertainties, to ensure coverage properties. To address this issue, we propose using a Quantile Regression Forest (QRF) to learn the distribution of nonconformity scores and utilizing the QRF's weights to assign more importance to samples with residuals similar to the test point. This approach results in PI lengths that are more aligned with the model's uncertainty. In addition, the weights learnt by the QRF provide a partition of the features space, allowing for more efficient computations and improved adaptiveness of the PI through groupwise conformalization. Our approach enjoys an assumption-free finite sample marginal and training-conditional coverage, and under suitable assumptions, it also ensures conditional coverage. Our methods work for any nonconformity score and are available as a Python package. We conduct experiments on simulated and real-world data that demonstrate significant improvements compared to existing methods.
翻译:尽管具有有吸引力的理论保证和实用成功的可能性,由一致性预测 (CP) 给出的预测区间 (PI) 可能无法反映模型的不确定性。这种局限性出现在 CP 方法为所有测试点使用常数校正,忽略它们的个体不确定性,以确保覆盖特性时。为了解决这个问题,我们建议使用量化回归森林 (QRF) 学习非一致性得分的分布,并利用 QRF 的权重为具有类似于测试点的残差的样本分配更多的重要性。这种方法导致了更符合模型不确定性的预测区间长度。此外,QRF 学到的权重提供了特征空间的一个分割,允许更有效的计算和通过分组一致化提高 PI 的适应性。我们的方法享有无假设的有限样本边缘和训练条件覆盖范围,并在适当的假设下也确保条件覆盖范围。我们的方法适用于任何非一致性分数,并作为 Python 包提供。我们对模拟和实际数据进行实验,结果显示与现有方法相比有显著的改进。