An Efficient Operator-Splitting Method for the Eigenvalue Problem of the Monge-Ampère Equation

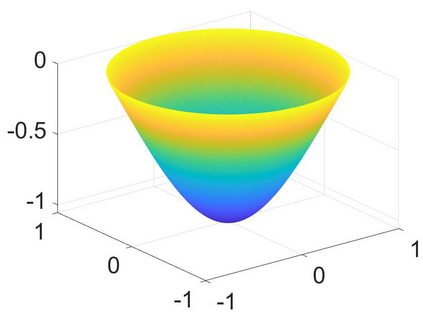
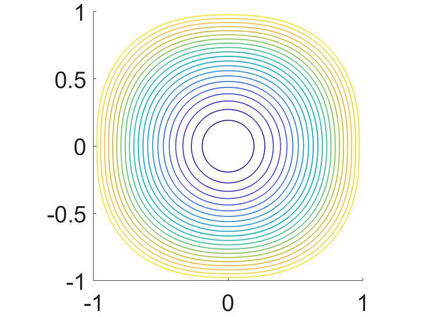
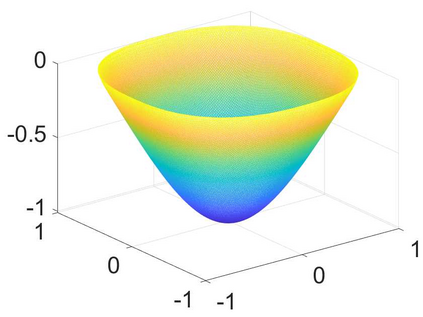
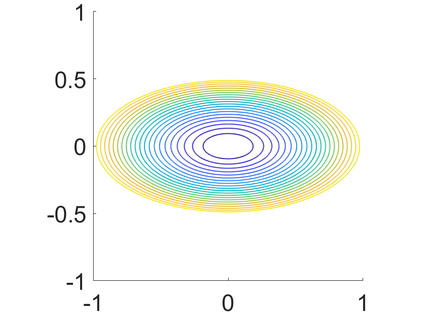
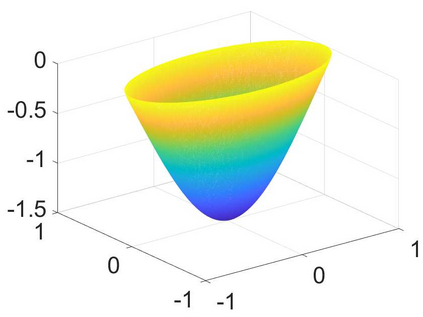
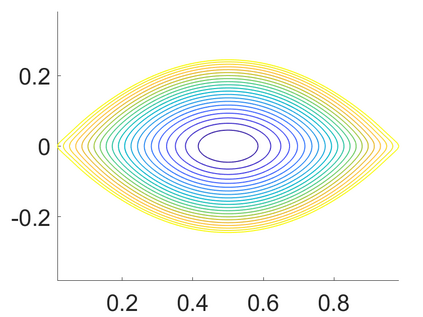
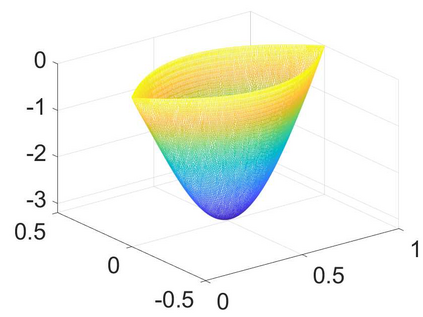
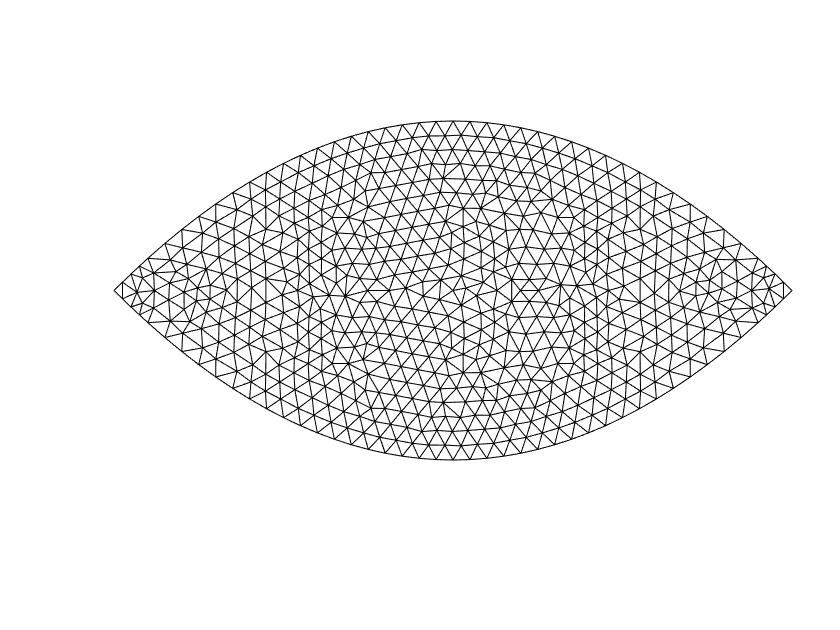
We develop an efficient operator-splitting method for the eigenvalue problem of the Monge-Amp\`{e}re operator in the Aleksandrov sense. The backbone of our method relies on a convergent Rayleigh inverse iterative formulation proposed by Abedin and Kitagawa (Inverse iteration for the {M}onge-{A}mp{\`e}re eigenvalue problem, {\it Proceedings of the American Mathematical Society}, 148 (2020), no. 11, 4975-4886). Modifying the theoretical formulation, we develop an efficient algorithm for computing the eigenvalue and eigenfunction of the Monge-Amp\`{e}re operator by solving a constrained Monge-Amp\`{e}re equation during each iteration. Our method consists of four essential steps: (i) Formulate the Monge-Amp\`{e}re eigenvalue problem as an optimization problem with a constraint; (ii) Adopt an indicator function to treat the constraint; (iii) Introduce an auxiliary variable to decouple the original constrained optimization problem into simpler optimization subproblems and associate the resulting new optimization problem with an initial value problem; and (iv) Discretize the resulting initial-value problem by an operator-splitting method in time and a mixed finite element method in space. The performance of our method is demonstrated by several experiments. Compared to existing methods, the new method is more efficient in terms of computational cost and has a comparable rate of convergence in terms of accuracy.