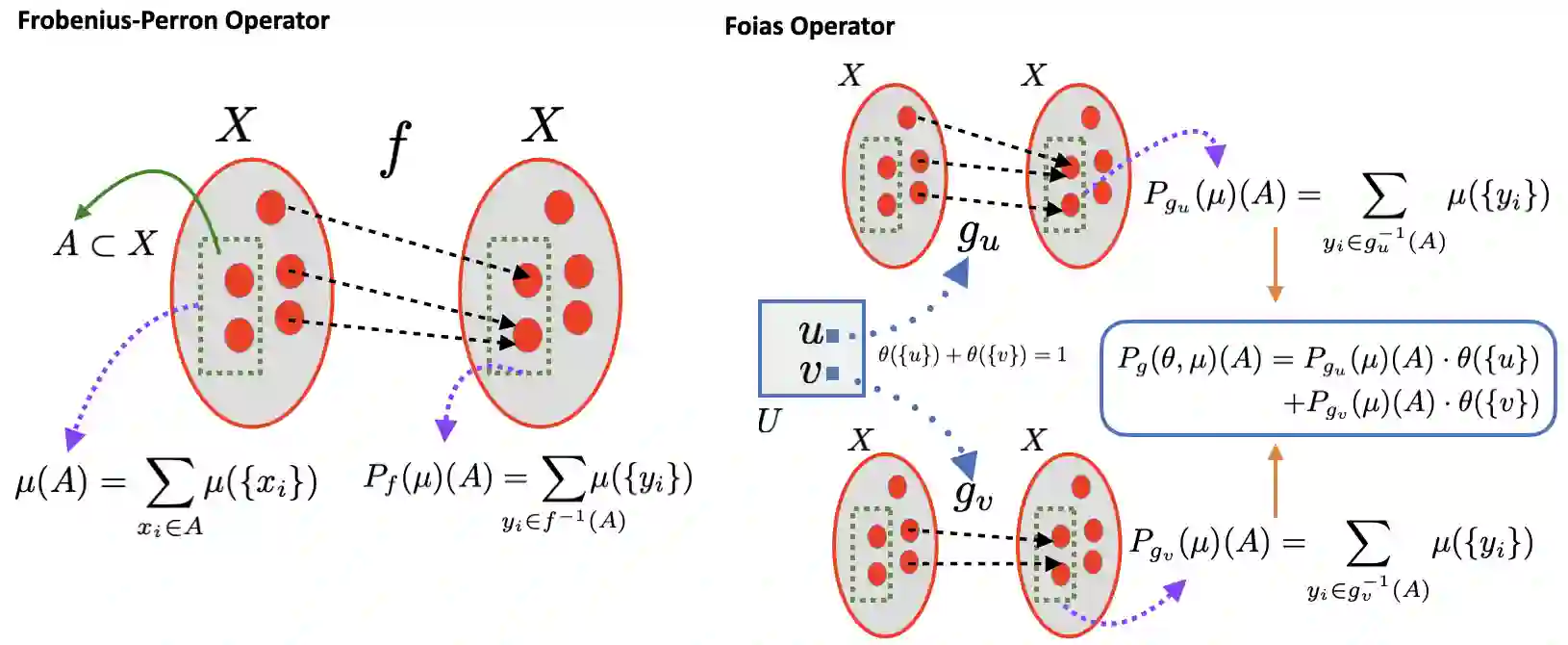
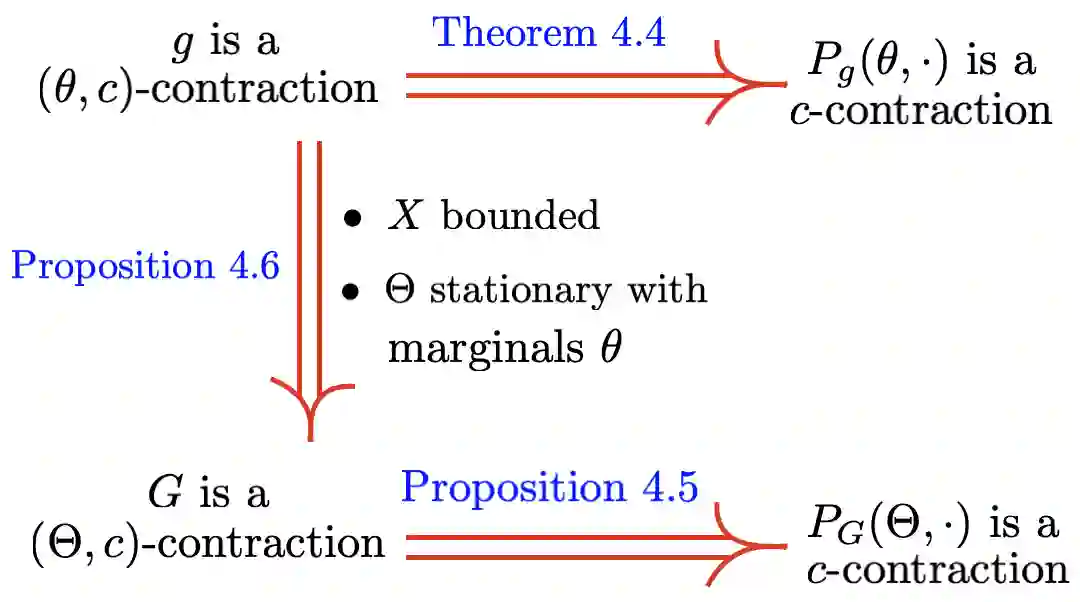
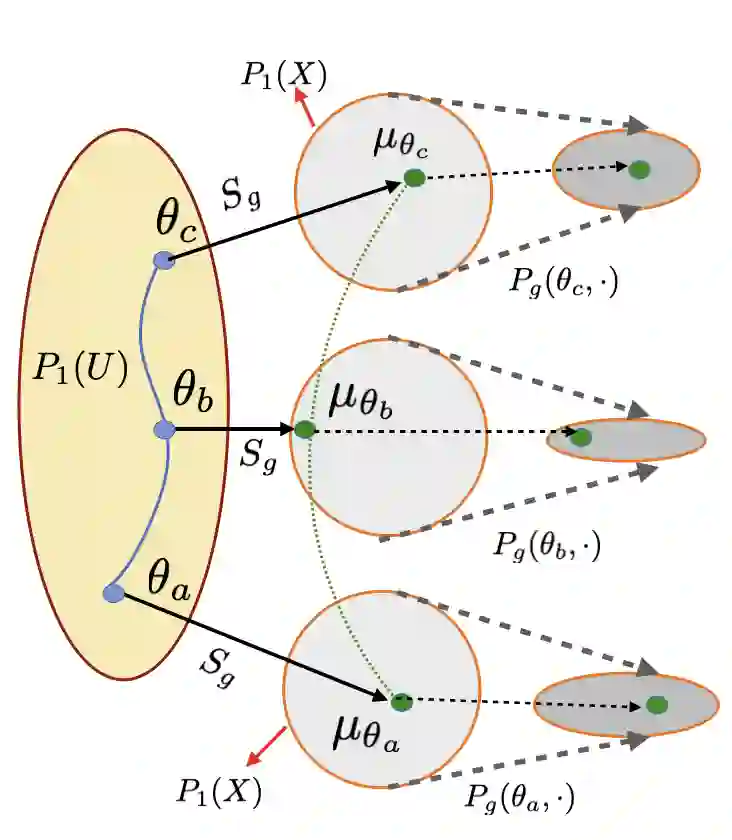
Reservoir computing systems are constructed using a driven dynamical system in which external inputs can alter the evolving states of a system. These paradigms are used in information processing, machine learning, and computation. A fundamental question that needs to be addressed in this framework is the statistical relationship between the input and the system states. This paper provides conditions that guarantee the existence and uniqueness of asymptotically invariant measures for driven systems and shows that their dependence on the input process is continuous when the set of input and output processes are endowed with the Wasserstein distance. The main tool in these developments is the characterization of those invariant measures as fixed points of naturally defined Foias operators that appear in this context and which have been profusely studied in the paper. Those fixed points are obtained by imposing a newly introduced stochastic state contractivity on the driven system that is readily verifiable in examples. Stochastic state contractivity can be satisfied by systems that are not state-contractive, which is a need typically evoked to guarantee the echo state property in reservoir computing. As a result, it may actually be satisfied even if the echo state property is not present.
翻译:储量计算系统是一个动态系统,外部投入可以改变一个系统的演变状态。这些范式用于信息处理、机器学习和计算。在这个框架内需要处理的一个根本问题是输入和系统状态之间的统计关系。本文件提供了一些条件,保证对驱动系统采取无变化的无源措施的存在和独特性,并表明当输入和产出流程被赋予瓦塞斯坦距离时,它们对输入过程的依赖是持续的。这些发展的主要工具是将这些变化性措施定性为自然定义的Foias操作者固定点,在这种背景下出现,并在文件中进行了大量研究。这些固定点是通过对驱动系统实行新引入的随机状态合同性来获得的,这种状态在实例中可以很容易地核实。不具有国家合同性的系统可以满足其对输入过程的依赖性,而这种系统通常是用来保证储油层计算中回声状态特性的一种需要。因此,即使回声状态财产不存在,也确实可以满足。