Virtual element method for elliptic bulk-surface PDEs in three space dimensions

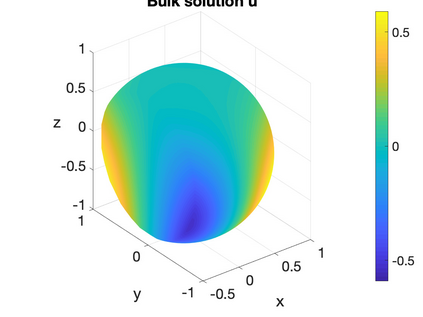
In this work we present a novel bulk-surface virtual element method (BSVEM) for the numerical approximation of elliptic bulk-surface partial differential equations (BSPDEs) in three space dimensions. The BSVEM is based on the discretisation of the bulk domain into polyhedral elements with arbitrarily many faces. The polyhedral approximation of the bulk induces a polygonal approximation of the surface. Firstly, we present a geometric error analysis of bulk-surface polyhedral meshes independent of the numerical method. Hence, we show that BSVEM has optimal second-order convergence in space, provided the exact solution is $H^{2+3/4}$ in the bulk and $H^2$ on the surface, where the additional $\frac{3}{4}$ is due to the combined effect of surface curvature and polyhedral elements close to the boundary. We show that general polyhedra can be exploited to reduce the computational time of the matrix assembly. To support our convergence results, a numerical example is presented which demonstrates optimal convergence of an elliptic BSPDE in three space dimensions.