On the achievability of blind source separation for high-dimensional nonlinear source mixtures

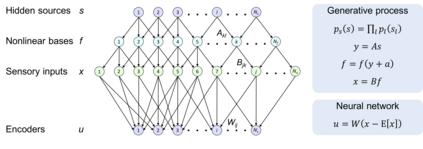
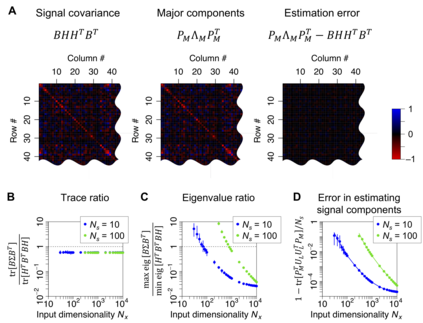
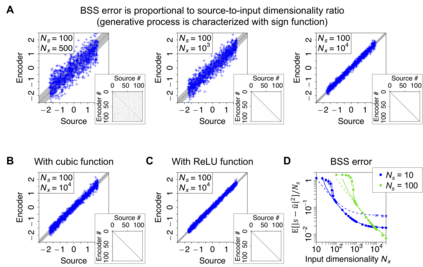
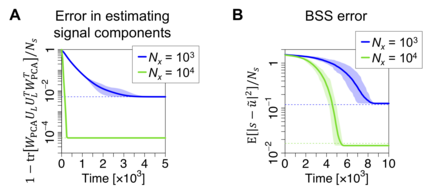
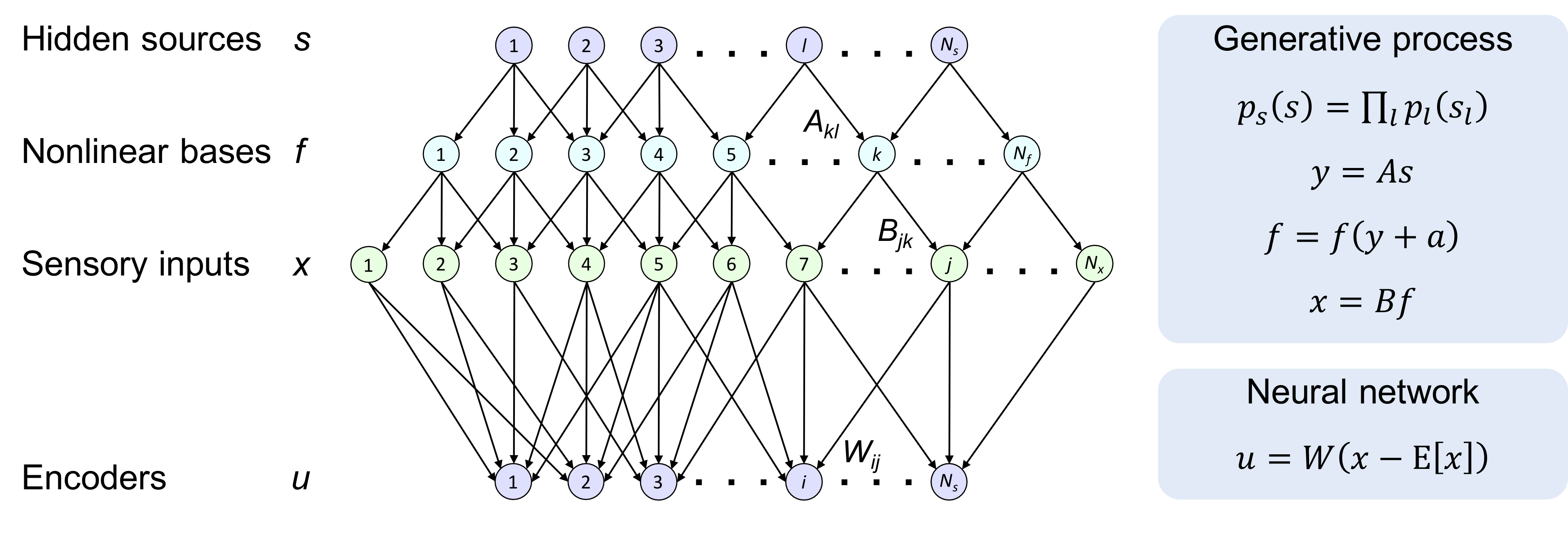
For many years, a combination of principal component analysis (PCA) and independent component analysis (ICA) has been used for blind source separation (BSS). However, it remains unclear why these linear methods work well with real-world data that involve nonlinear source mixtures. This work theoretically validates that a cascade of linear PCA and ICA can solve a nonlinear BSS problem accurately -- when the sensory inputs are generated from hidden sources via nonlinear mappings with sufficient dimensionality. Our proposed theorem, termed the asymptotic linearization theorem, theoretically guarantees that applying linear PCA to the inputs can reliably extract a subspace spanned by the linear projections from every hidden source as the major components -- and thus projecting the inputs onto their major eigenspace can effectively recover a linear transformation of the hidden sources. Then, subsequent application of linear ICA can separate all the true independent hidden sources accurately. Zero-element-wise-error nonlinear BSS is asymptotically attained when the source dimensionality is large and the input dimensionality is sufficiently larger than the source dimensionality. Our proposed theorem is validated analytically and numerically. Moreover, the same computation can be performed by using Hebbian-like plasticity rules, implying the biological plausibility of this nonlinear BSS strategy. Our results highlight the utility of linear PCA and ICA for accurately and reliably recovering nonlinearly mixed sources -- and further suggest the importance of employing sensors with sufficient dimensionality to identify true hidden sources of real-world data.