Enabling and interpreting hyper-differential sensitivity analysis for Bayesian inverse problems

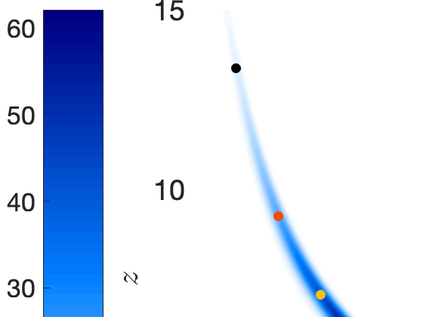
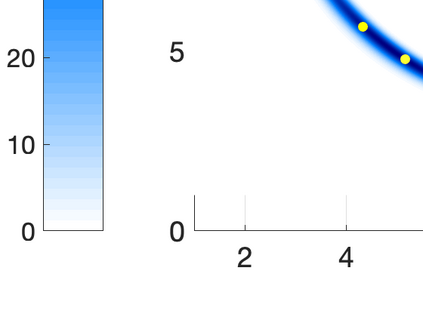
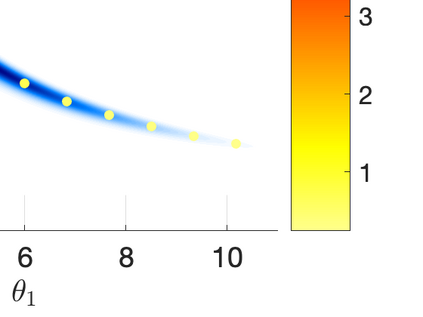
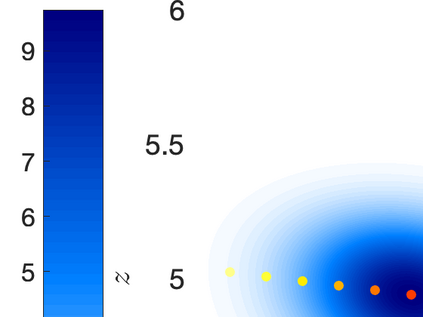
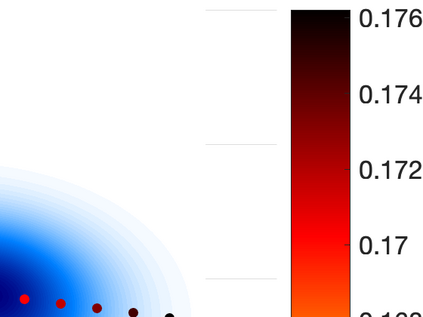
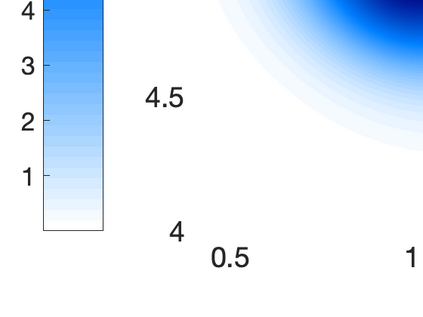
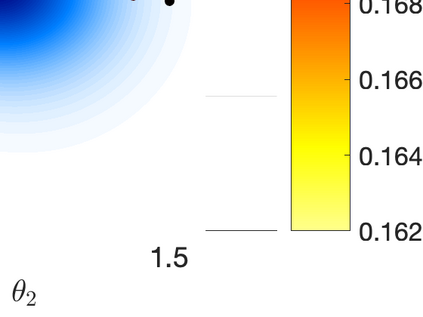
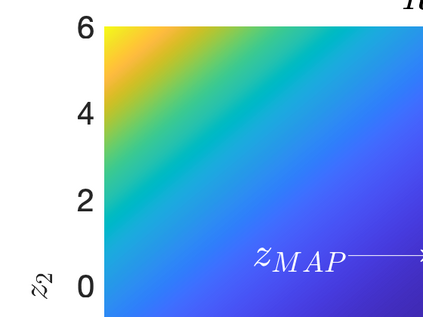
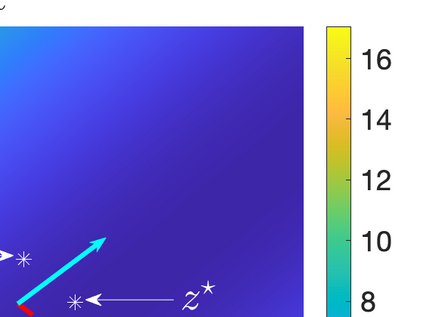
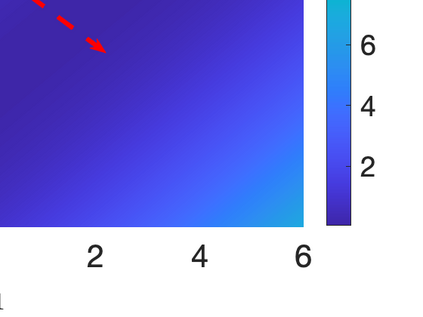
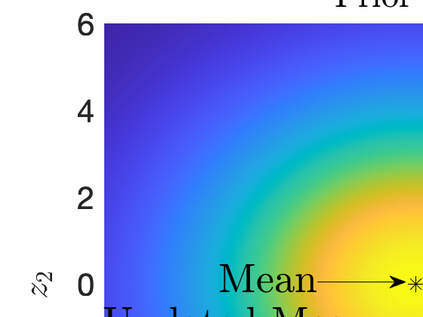
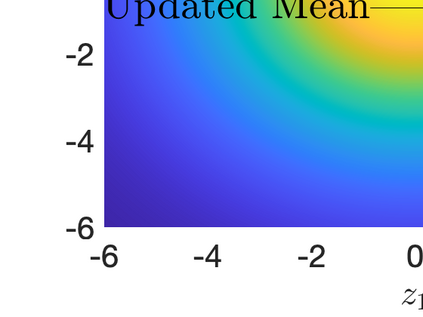
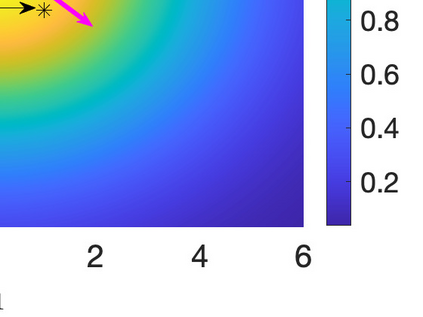
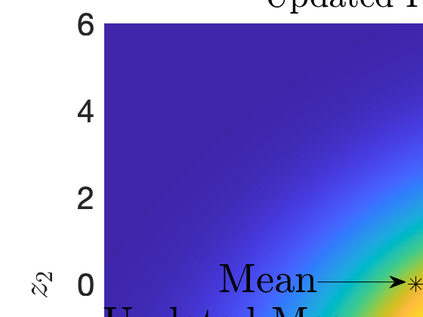
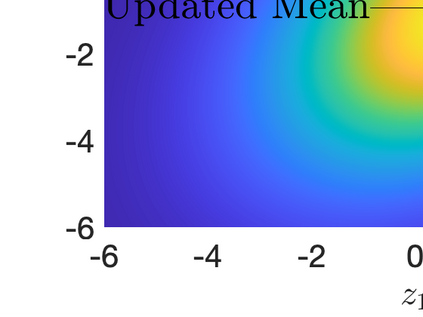
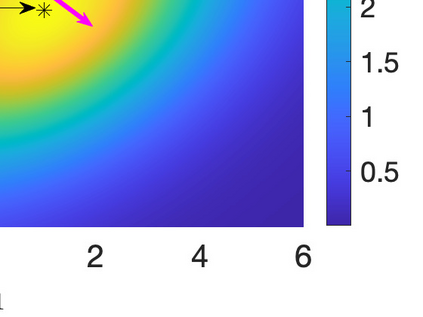
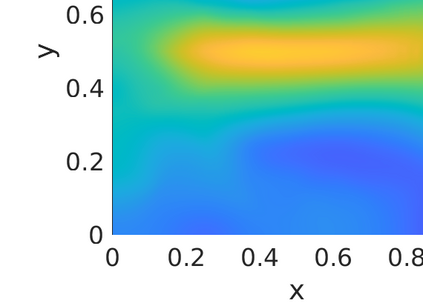
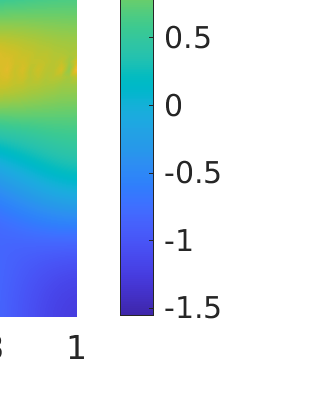
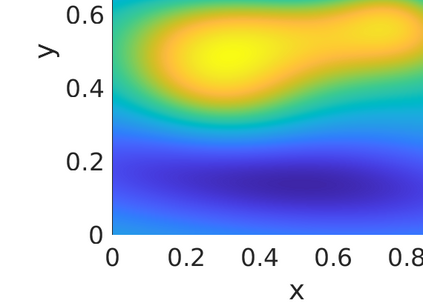
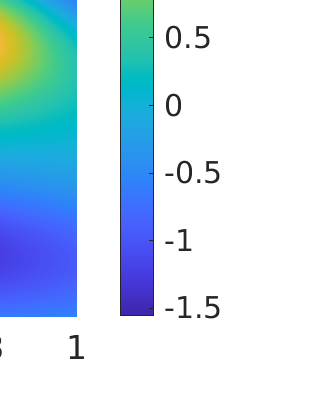
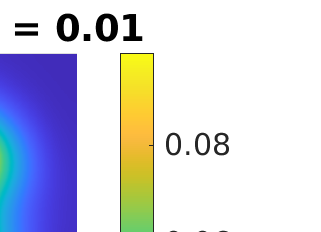
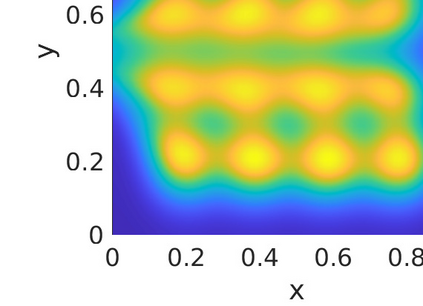
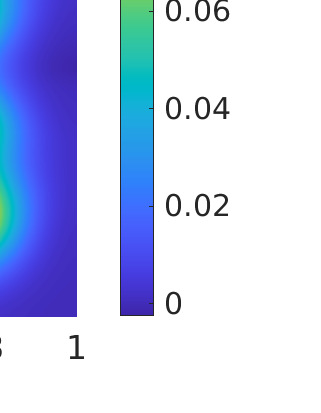
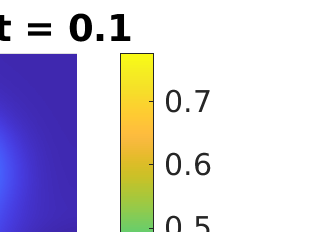
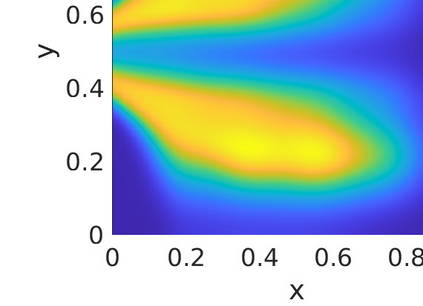
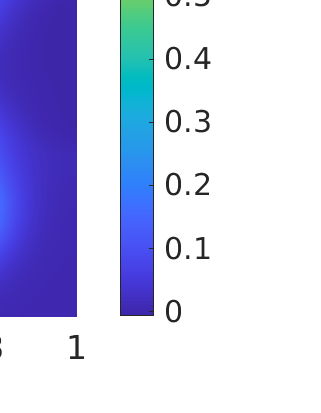
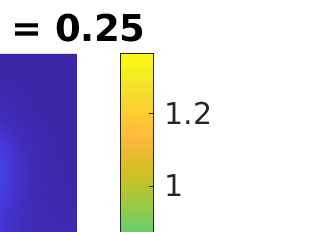
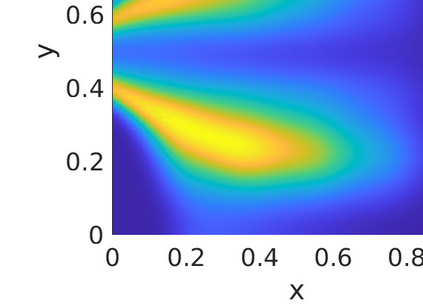
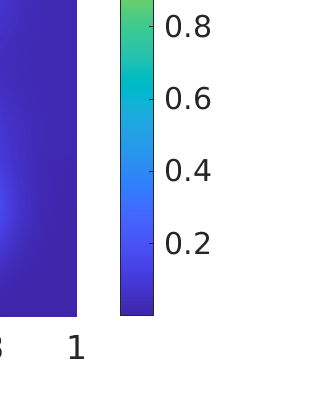
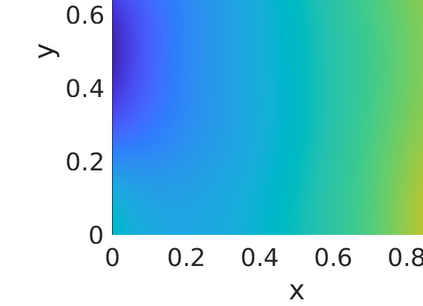
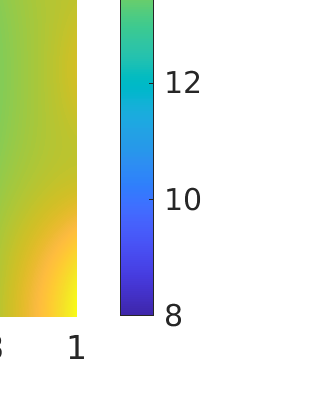
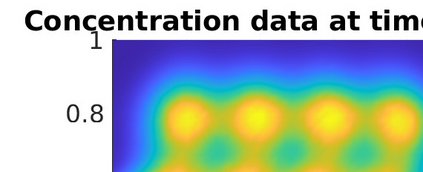
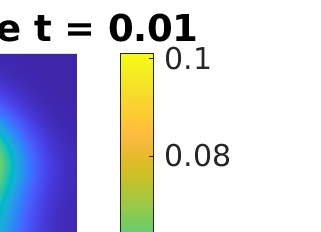
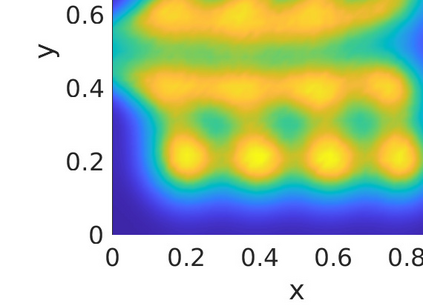
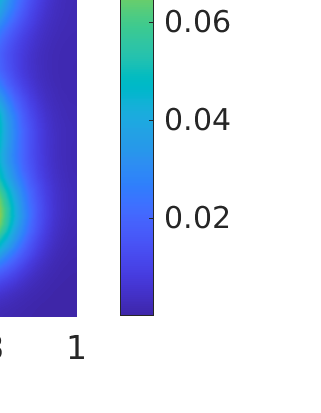
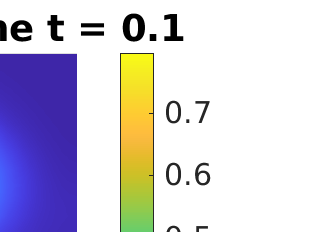
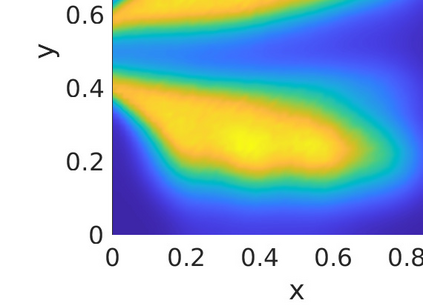
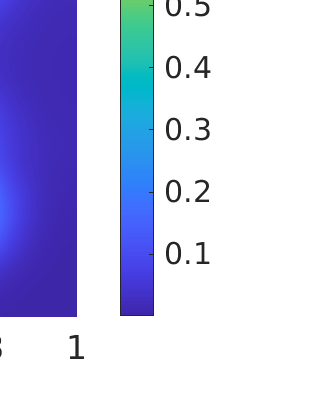
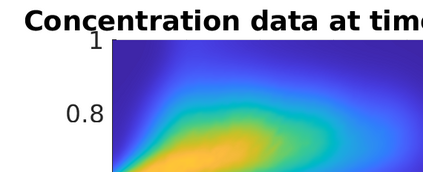
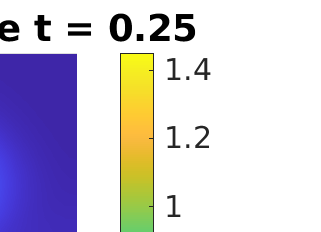
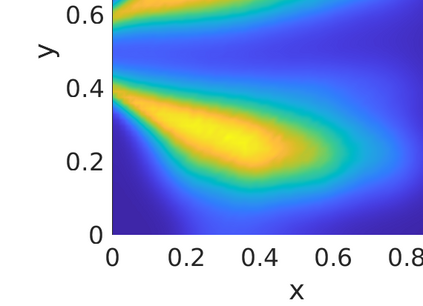
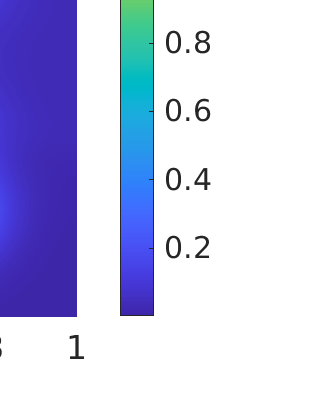
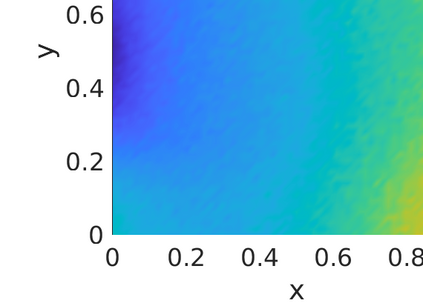
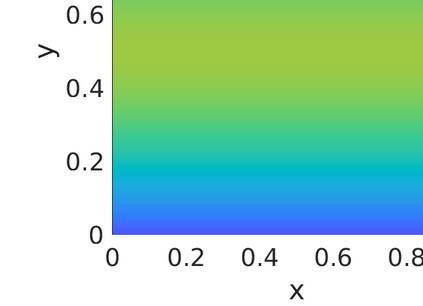
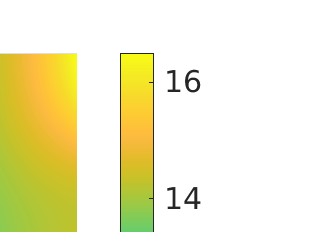Inverse problems constrained by partial differential equations (PDEs) play a critical role in model development and calibration. In many applications, there are multiple uncertain parameters in a model which must be estimated. Although the Bayesian formulation is attractive for such problems, computational cost and high dimensionality frequently prohibit a thorough exploration of the parametric uncertainty. A common approach is to reduce the dimension by fixing some parameters (which we will call auxiliary parameters) to a best estimate and using techniques from PDE-constrained optimization to approximate properties of the Bayesian posterior distribution. For instance, the maximum a posteriori probability (MAP) and the Laplace approximation of the posterior covariance can be computed. In this article, we propose using hyper-differential sensitivity analysis (HDSA) to assess the sensitivity of the MAP point to changes in the auxiliary parameters. We establish an interpretation of HDSA as correlations in the posterior distribution. Foundational assumptions for HDSA require satisfaction of the optimality conditions which are not always feasible or appropriate as a result of ill-posedness in the inverse problem. We introduce novel theoretical and computational approaches to justify and enable HDSA for ill-posed inverse problems by projecting the sensitivities on likelihood informed subspaces and defining a posteriori updates. Our proposed framework is demonstrated on a nonlinear multi-physics inverse problem motivated by estimation of spatially heterogenous material properties in the presence of spatially distributed parametric modeling uncertainties.