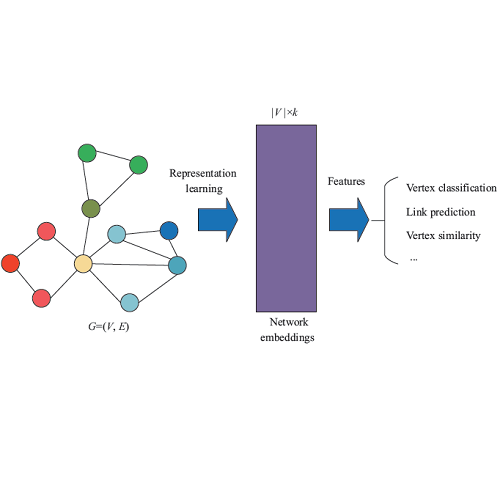
Network representation learning (NRL) technique has been successfully adopted in various data mining and machine learning applications. Random walk based NRL is one popular paradigm, which uses a set of random walks to capture the network structural information, and then employs word2vec models to learn the low-dimensional representations. However, until now there is lack of a framework, which unifies existing random walk based NRL models and supports to efficiently learn from large networks. The main obstacle comes from the diverse random walk models and the inefficient sampling method for the random walk generation. In this paper, we first introduce a new and efficient edge sampler based on Metropolis-Hastings sampling technique, and theoretically show the convergence property of the edge sampler to arbitrary discrete probability distributions. Then we propose a random walk model abstraction, in which users can easily define different transition probability by specifying dynamic edge weights and random walk states. The abstraction is efficiently supported by our edge sampler, since our sampler can draw samples from unnormalized probability distribution in constant time complexity. Finally, with the new edge sampler and random walk model abstraction, we carefully implement a scalable NRL framework called UniNet. We conduct comprehensive experiments with five random walk based NRL models over eleven real-world datasets, and the results clearly demonstrate the efficiency of UniNet over billion-edge networks.
翻译:在各种数据挖掘和机器学习应用中成功采用了基于随机步行的网络代表学习(NRL)技术。基于随机行走的NRL是一种流行范例,它使用一套随机行走来捕捉网络结构信息,然后使用单词2vec模型来学习低维表达方式。然而,直到现在,还缺乏一个框架,将现有的随机行走的NRL模型统一起来,支持从大型网络中有效学习。主要障碍来自各种随机行走模型和随机行走生成的低效率抽样方法。在本文中,我们首先采用一个新的高效边缘取样器,以Metopolis-Hastings取样技术为基础,并在理论上显示边缘取样器的趋同属性,以任意的离散概率分布。然后我们提出一个随机行走模型抽象化模型,用户可以在其中通过指定动态边权重和随机行走状态来轻松定义不同的过渡概率。这个抽象化模型得到我们的边缘取样器的有效支持,因为我们的取样员可以从不固定时间复杂性的概率分布中提取样本。最后,我们通过新的边缘取样器和随机行走模型,从任意行走模型,我们谨慎地用一个可测量的RRRRRWlL框架,我们用了一个对5级的综合模型进行。