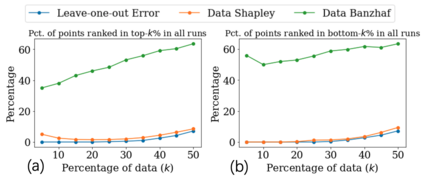
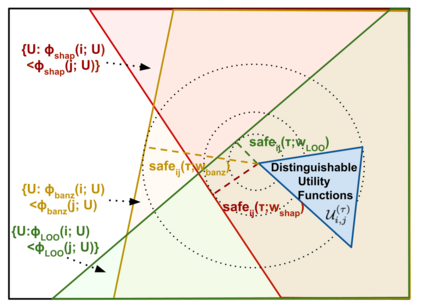
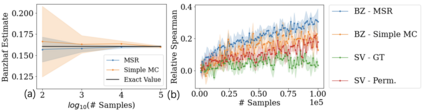
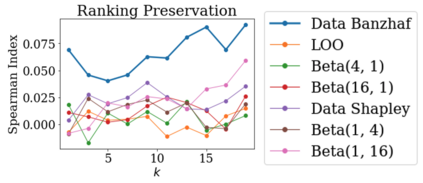
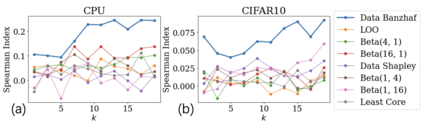
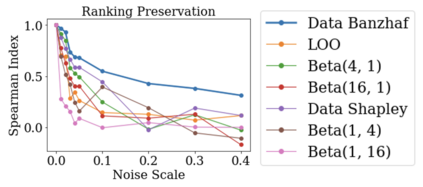
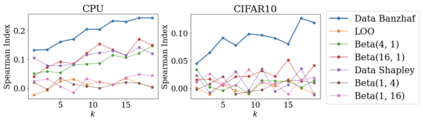
Data valuation has wide use cases in machine learning, including improving data quality and creating economic incentives for data sharing. This paper studies the robustness of data valuation to noisy model performance scores. Particularly, we find that the inherent randomness of the widely used stochastic gradient descent can cause existing data value notions (e.g., the Shapley value and the Leave-one-out error) to produce inconsistent data value rankings across different runs. To address this challenge, we introduce the concept of safety margin, which measures the robustness of a data value notion. We show that the Banzhaf value, a famous value notion that originated from cooperative game theory literature, achieves the largest safety margin among all semivalues (a class of value notions that satisfy crucial properties entailed by ML applications and include the famous Shapley value and Leave-one-out error). We propose an algorithm to efficiently estimate the Banzhaf value based on the Maximum Sample Reuse (MSR) principle. Our evaluation demonstrates that the Banzhaf value outperforms the existing semivalue-based data value notions on several ML tasks such as learning with weighted samples and noisy label detection. Overall, our study suggests that when the underlying ML algorithm is stochastic, the Banzhaf value is a promising alternative to the other semivalue-based data value schemes given its computational advantage and ability to robustly differentiate data quality.
翻译:在机器学习中,数据估值具有广泛应用的案例,包括提高数据质量和为数据共享创造经济激励因素。本文件研究数据估值的稳健性,以得出吵闹的模型性能评分。特别是,我们发现,广泛使用的随机性梯度梯度下降的内在随机性可造成现有数据价值概念(如沙普利值和放假一出差错),在不同运行中产生不一致的数据价值排名。为了应对这一挑战,我们引入了安全比值概念,以衡量数据价值概念的稳健性。我们表明,Banzhaf值,即源自合作游戏理论文献的著名价值概念,在所有半值中取得了最大的安全比值(一类价值概念,满足了ML应用程序带来的关键特性,包括著名的沙普利值和放假一出差差差差差差差差差差差差差),可导致不同运行的数据价值排名不一致。我们提出的一个算法是,根据最大采样再用原则(Mzhaf)衡量现有半值数据价值概念,即学习加权样品和焦压半标签质量能力,总体而言,我们的研究显示,其高估值的基值为其他数据比重数据。</s>