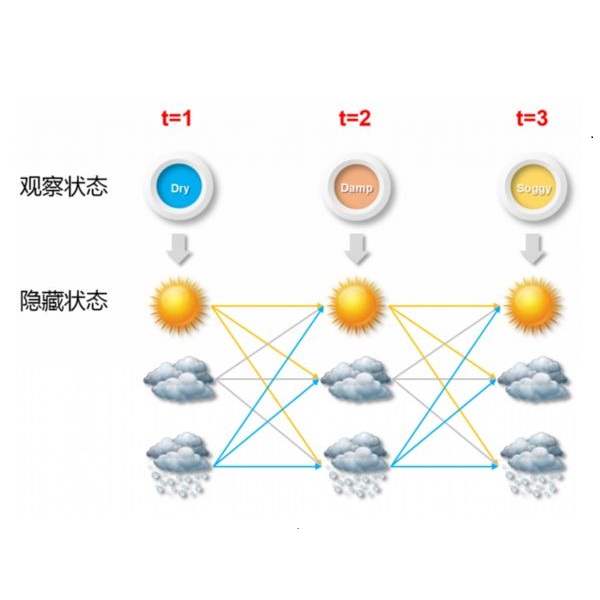
Hidden Markov Models (HMMs) comprise a powerful generative approach for modeling sequential data and time-series in general. However, the commonly employed assumption of the dependence of the current time frame to a single or multiple immediately preceding frames is unrealistic; more complicated dynamics potentially exist in real world scenarios. This paper revisits conventional sequential modeling approaches, aiming to address the problem of capturing time-varying temporal dependency patterns. To this end, we propose a different formulation of HMMs, whereby the dependence on past frames is dynamically inferred from the data. Specifically, we introduce a hierarchical extension by postulating an additional latent variable layer; therein, the (time-varying) temporal dependence patterns are treated as latent variables over which inference is performed. We leverage solid arguments from the Variational Bayes framework and derive a tractable inference algorithm based on the forward-backward algorithm. As we experimentally show, our approach can model highly complex sequential data and can effectively handle data with missing values.
翻译:隐藏的 Markov 模型( HMMS ) 包含一个强大的基因化方法, 用于建模顺序数据和一般的时间序列。 但是, 通常采用的假设, 即当前时间框架对前一个或多个框架的依赖性是不现实的; 更复杂的动态在现实世界情景中可能存在。 本文重审常规的顺序模型方法, 旨在解决捕捉时间变化的暂时依赖性模式问题。 为此, 我们建议了不同的 HMMs 配方, 从而动态地从数据中推断对过去框架的依赖性。 具体地说, 我们采用一个等级的扩展, 假设额外的潜伏变量层; 其中, (时间变化的) 时间依赖性模式被视为潜在的变量, 进行推断。 我们利用Varigational Bayes 框架的坚实论据, 并得出基于前向后向算法的可引导算算法。 正如我们实验显示的那样, 我们的方法可以建模高度复杂的连续数据, 并有效地处理缺少值的数据 。