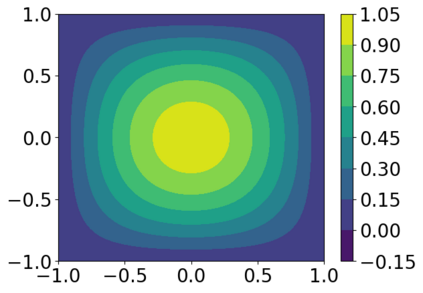
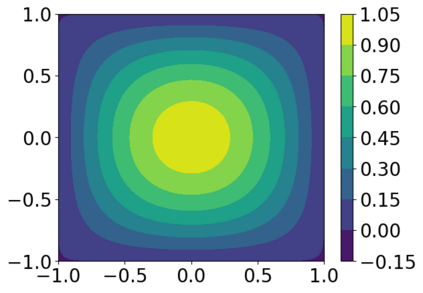
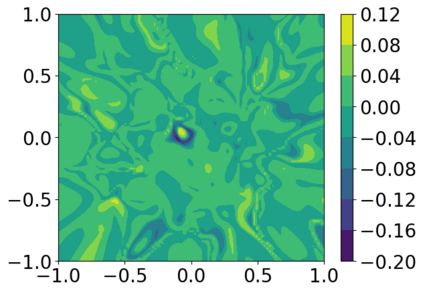
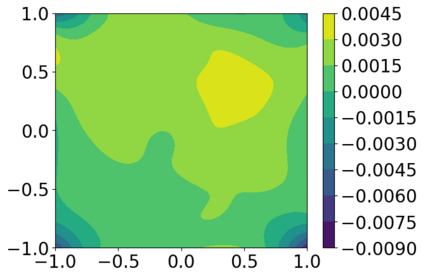
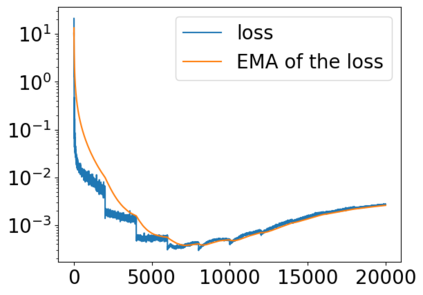
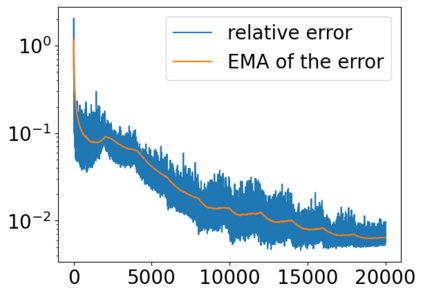
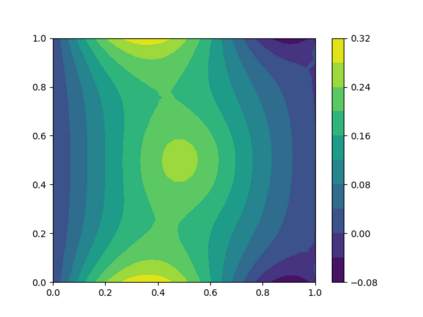
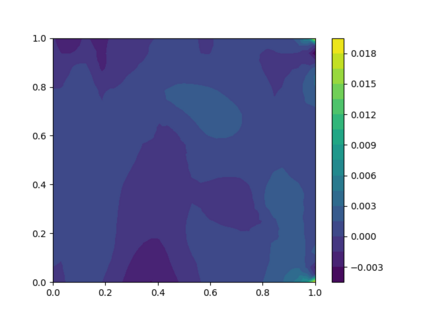
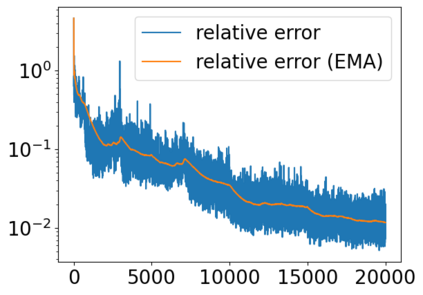
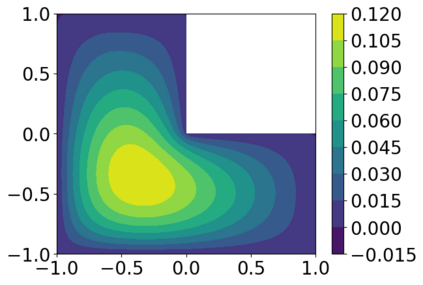
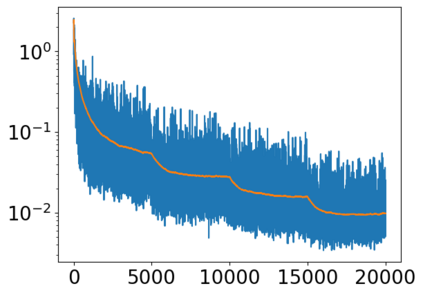
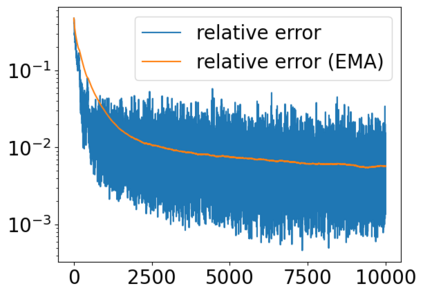
Solving high dimensional partial differential equations (PDEs) has historically posed a considerable challenge when utilizing conventional numerical methods, such as those involving domain meshes. Recent advancements in the field have seen the emergence of neural PDE solvers, leveraging deep networks to effectively tackle high dimensional PDE problems. This study introduces Inf-SupNet, a model-based unsupervised learning approach designed to acquire solutions for a specific category of elliptic PDEs. The fundamental concept behind Inf-SupNet involves incorporating the inf-sup formulation of the underlying PDE into the loss function. The analysis reveals that the global solution error can be bounded by the sum of three distinct errors: the numerical integration error, the duality gap of the loss function (training error), and the neural network approximation error for functions within Sobolev spaces. To validate the efficacy of the proposed method, numerical experiments conducted in high dimensions demonstrate its stability and accuracy across various boundary conditions, as well as for both semi-linear and nonlinear PDEs.
翻译:暂无翻译