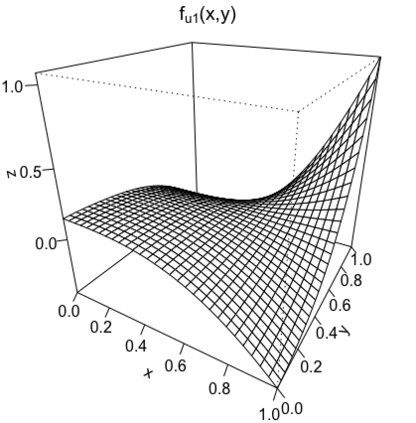
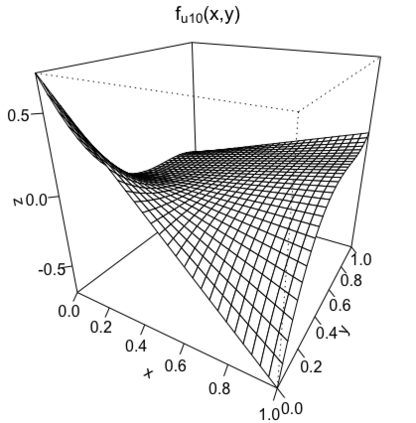
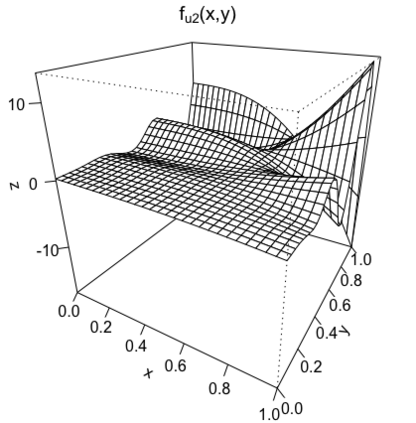
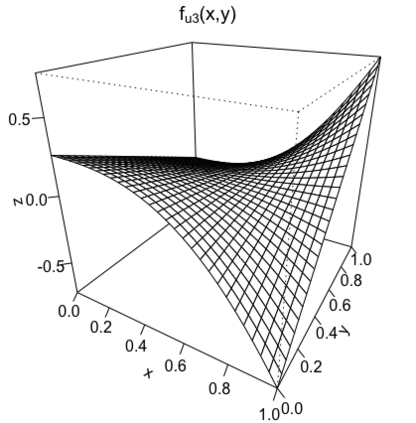
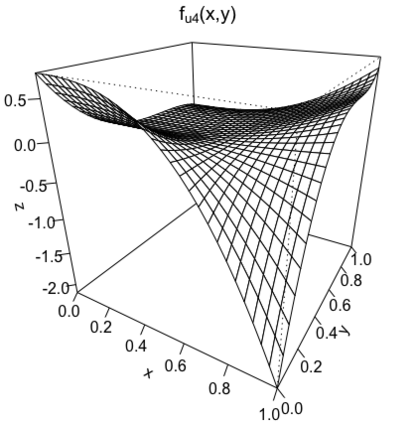
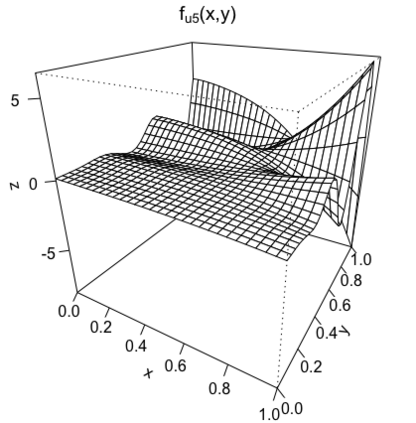
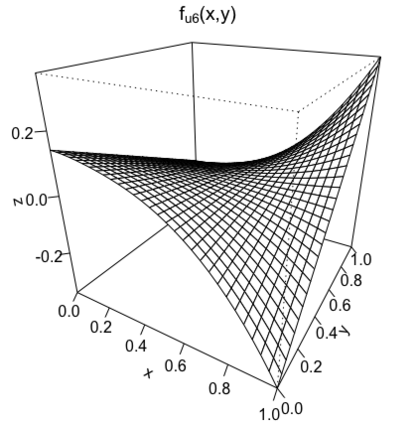
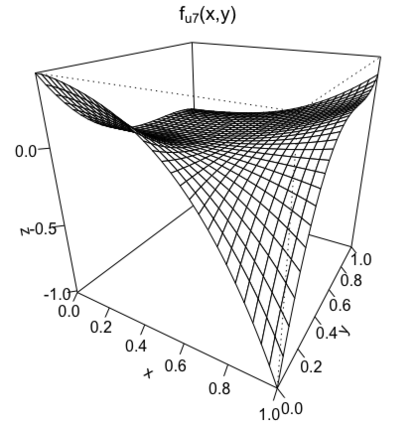
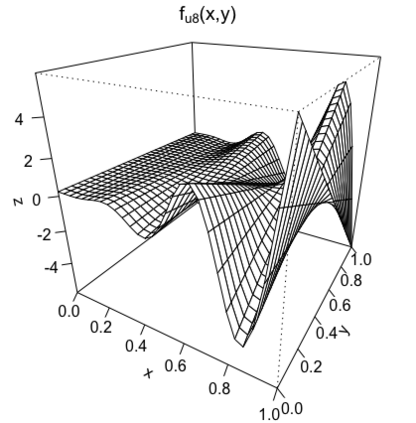
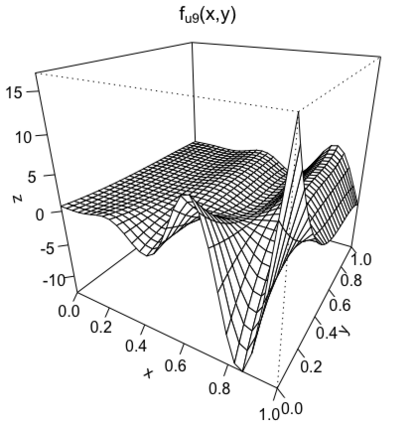
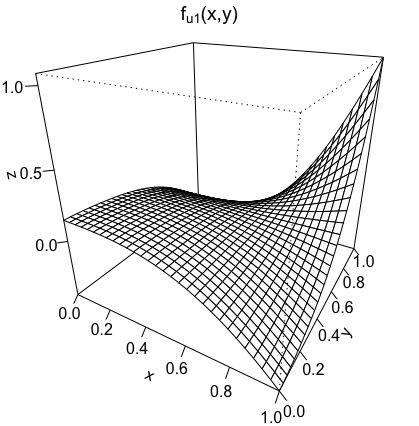
We study the problem of adaptive variable selection in a Gaussian white noise model of intensity $\varepsilon$ under certain sparsity and regularity conditions on an unknown regression function $f$. The $d$-variate regression function $f$ is assumed to be a sum of functions each depending on a smaller number $k$ of variables ($1 \leq k \leq d$). These functions are unknown to us and only few of them are nonzero. We assume that $d=d_\varepsilon \to \infty$ as $\varepsilon \to 0$ and consider the cases when $k$ is fixed and when $k=k_\varepsilon \to \infty$, $k=o(d)$ as $\varepsilon \to 0$. In this work, we introduce an adaptive selection procedure that, under some model assumptions, identifies exactly all nonzero $k$-variate components of $f$. In addition, we establish conditions under which exact identification of the nonzero components is impossible. These conditions ensure that the proposed selection procedure is the best possible in the asymptotically minimax sense with respect to the Hamming risk.
翻译:暂无翻译