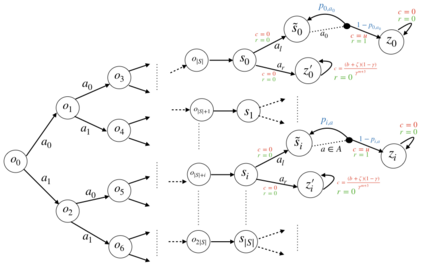
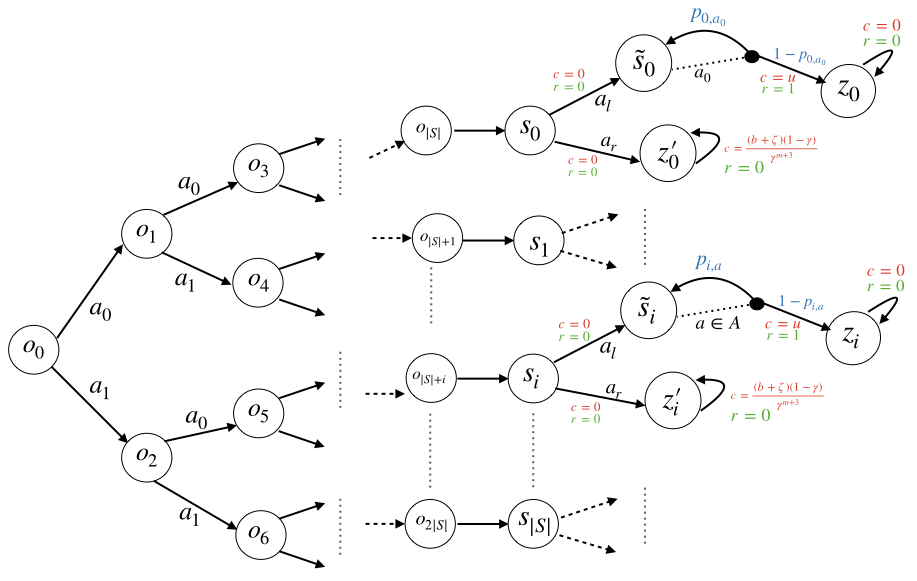
In contrast to the advances in characterizing the sample complexity for solving Markov decision processes (MDPs), the optimal statistical complexity for solving constrained MDPs (CMDPs) remains unknown. We resolve this question by providing minimax upper and lower bounds on the sample complexity for learning near-optimal policies in a discounted CMDP with access to a generative model (simulator). In particular, we design a model-based algorithm that addresses two settings: (i) relaxed feasibility, where small constraint violations are allowed, and (ii) strict feasibility, where the output policy is required to satisfy the constraint. For (i), we prove that our algorithm returns an $\epsilon$-optimal policy with probability $1 - \delta$, by making $\tilde{O}\left(\frac{S A \log(1/\delta)}{(1 - \gamma)^3 \epsilon^2}\right)$ queries to the generative model, thus matching the sample-complexity for unconstrained MDPs. For (ii), we show that the algorithm's sample complexity is upper-bounded by $\tilde{O} \left(\frac{S A \, \log(1/\delta)}{(1 - \gamma)^5 \, \epsilon^2 \zeta^2} \right)$ where $\zeta$ is the problem-dependent Slater constant that characterizes the size of the feasible region. Finally, we prove a matching lower-bound for the strict feasibility setting, thus obtaining the first near minimax optimal bounds for discounted CMDPs. Our results show that learning CMDPs is as easy as MDPs when small constraint violations are allowed, but inherently more difficult when we demand zero constraint violation.
翻译:与解决 Markov 决策程序( MDPs) 的样本复杂性特征相比, 解决受限制的 MDP (CMDPs) 的最佳统计复杂性仍然未知。 我们解决这个问题的方法是, 在折扣的 CMDP 中提供用于学习近最佳政策的样本复杂性上下界限, 使用基因化模型( 模拟器) 。 特别是, 我们设计一种基于模型的算法, 处理两种设置 :( 一) 放松可行性, 允许小节制违约, 和 (二) 严格的可行性, 需要输出政策来满足制约。 (一) 我们证明我们的算法返回了 $\ epslon$- 最佳政策, 概率为 1 -\ delta$; 我们证明, $\\\\\\ left (ferc{ S\ 小型 =log (1/ deltata) { (1- gammamamamamamamama) 中, 当我们无法进行精度测试时, 最优的MDPs (r2\\\ main remax remax) max a res remax relial res remax max max max s max lax s lax lax s lax the lax lax lax lax lax s lax s lax s lax s lax s lax s lax s lax lax lax lax lax s lax lax lax lax lax lax lax lax lax lax lax lax lax lax lax lax lax lax lax lax) lax lax lads lax lad lad lax lax lax lax lax lads lax lax lax lads lax lax lax lax lads lax lads lads lads lax) lax)