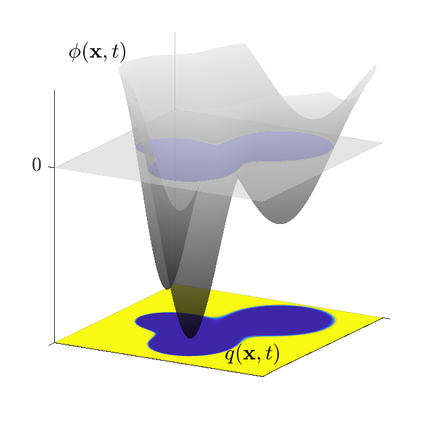
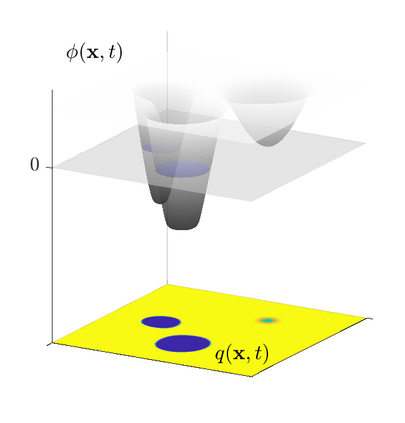
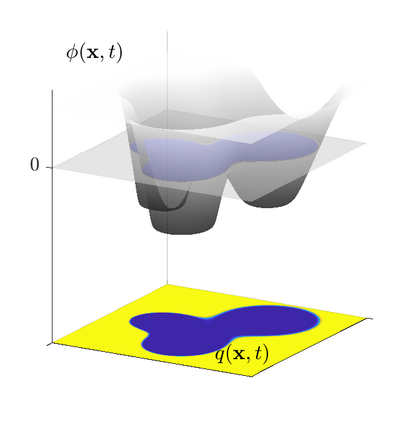
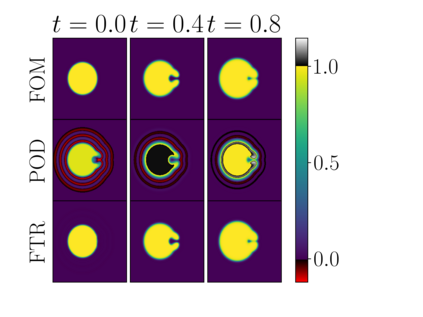
This work addresses model order reduction for complex moving fronts, which are transported by advection or through a reaction-diffusion process. Such systems are especially challenging for model order reduction since the transport cannot be captured by linear reduction methods. Moreover, topological changes, such as splitting or merging of fronts pose difficulties for many nonlinear reduction methods and the small non-vanishing support of the underlying partial differential equations dynamics makes most nonlinear hyper-reduction methods infeasible. We propose a new decomposition method together with a hyper-reduction scheme that addresses these shortcomings. The decomposition uses a level-set function to parameterize the transport and a nonlinear activation function that captures the structure of the front. This approach is similar to autoencoder artificial neural networks, but additionally provides insights into the system, which can be used for efficient reduced order models. We make use of this property and are thus able to solve the advection equation with the same complexity as the POD-Galerkin approach while obtaining errors of less than one percent for representative examples. Furthermore, we outline a special hyper-reduction method for more complicated advection-reaction-diffusion systems. The capability of the approach is illustrated by various numerical examples in one and two spatial dimensions, including real-life applications to a two-dimensional Bunsen flame.
翻译:这项工作针对的是复杂的移动战线的降序模式,通过平流或反扩散过程运输这些复杂移动战线的降序模式。这些系统对于降序模式特别具有挑战性,因为运输无法通过线性削减方法捕获。此外,诸如分解或合并战线等地形变化给许多非线性削减方法带来了困难,而对基础部分差异方程式动态的小规模非优势支持则使得大多数非线性超减法不可行。我们提出了一种新的分解方法,同时提出了解决这些缺陷的超级削减办法。这种分解利用了水平定值功能来参数化运输和非线性激活功能,从而捕捉到前线的结构。这一方法类似于自动变形人为神经网络,但进一步提供了对系统的洞察力,可用于高效的减少定序模型。我们利用了这种属性,从而能够以与POD-Galkin方法同样的复杂性解决反向方方方方程式,同时获得比有代表性的例子差1%的误差。此外,我们用一种特殊的超标法化超标法化方法来将运输和非线性激活前导体激活前线性线性神经网络的功能。这个方法类似于自动造神经系统,通过两种变式的系统,包括一种数字式的软模模制模化的模模模化的系统。