Regret Analysis of Certainty Equivalence Policies in Continuous-Time Linear-Quadratic Systems

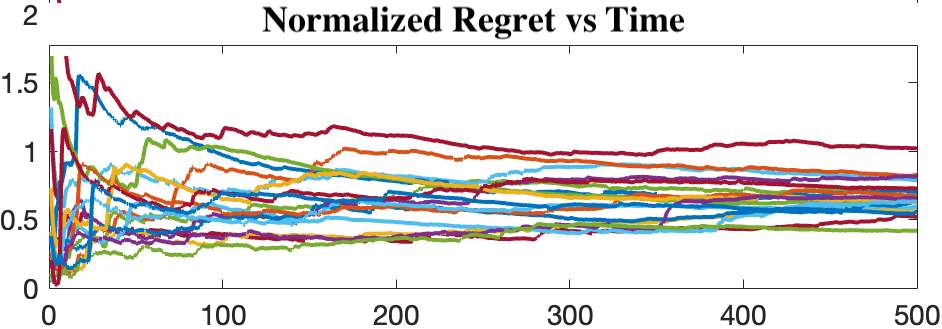
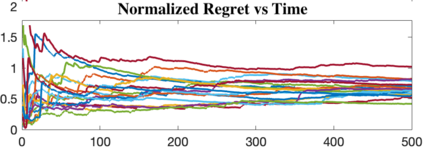
This work theoretically studies a ubiquitous reinforcement learning policy for controlling the canonical model of continuous-time stochastic linear-quadratic systems. We show that randomized certainty equivalent policy addresses the exploration-exploitation dilemma in linear control systems that evolve according to unknown stochastic differential equations and their operating cost is quadratic. More precisely, we establish square-root of time regret bounds, indicating that randomized certainty equivalent policy learns optimal control actions fast from a single state trajectory. Further, linear scaling of the regret with the number of parameters is shown. The presented analysis introduces novel and useful technical approaches, and sheds light on fundamental challenges of continuous-time reinforcement learning.