Generalised Bayesian Structural Equation Modelling

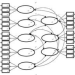
We propose a generalised framework for Bayesian Structural Equation Modelling (SEM) that can be applied to a variety of data types. The introduced framework focuses on the approximate zero approach, according to which parameters that would before set to zero (e.g. factor loadings) are now formulated to be approximate zero. It extends previously suggested models by \citeA{MA12} and can handle continuous, binary, and ordinal data. Moreover, we propose a novel model assessment paradigm aiming to address shortcomings of posterior predictive $p-$values, which provide the default metric of fit for Bayesian SEM. The introduced model assessment procedure monitors the out-of-sample predictive performance of the fitted model, and together with a list of guidelines we provide, one can investigate whether the hypothesised model is supported by the data. We incorporate scoring rules and cross-validation to supplement existing model assessment metrics for Bayesian SEM. We study the performance of the proposed methodology via simulations. The model for continuous and binary data is fitted to data on the `Big-5' personality scale and the Fagerstrom test for nicotine dependence respectively.