Inferring Parsimonious Coupling Statistics in Nonlinear Dynamics with Variational Gaussian Processes

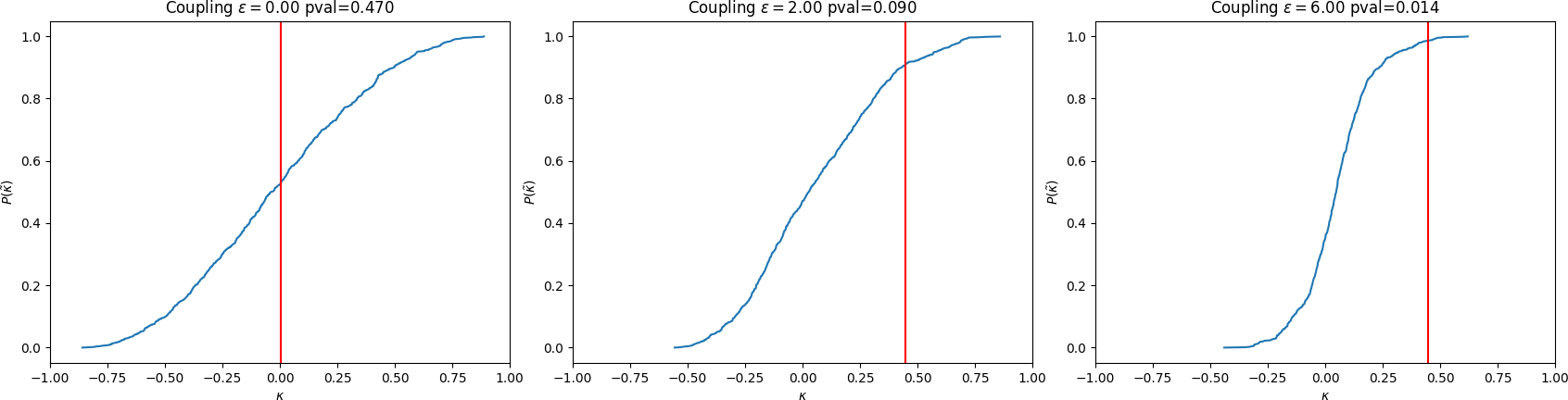
Nonparametric methods of uncovering coupling provides a flexible framework for researchers to study network configurations and discover causal graphs. For example, Gaussian Processes have been applied to discover coupling in dynamical systems under the convergent cross-mapping (GP-CCM) framework. Though GP-CCM is a nonparametric method, a function of the data, variations in hyperparameters may impact model results. Maximum marginal likelihood is commonly used to optimize such hyperparameters, however only point estimates are provided from such a routine. In this work, we determine a posteriori the hyperparameter distribution conditioned on the data by the use of variational Bayesian methods with mean field approximations on the posterior distribution of the hyperparameters, thus introducing the variational form of Gaussian process convergent cross-mapping (VGP-CCM). We show that using the a posteriori best approximate model that maximizes evidence of the data for hyperparameters sampling in VGP-CCM, in conjunction with a permutation sampling for the null distribution of uncoupled time series, permits significance statistics that are more robust than mere permutation sampling of the null GP-CCM distribution. We perform tests on synthetic data derived from unidirectionally coupled Lorenz-Rossler systems to demonstrate that the proposed method yields substantially improved specificity over the original GP-CCM.