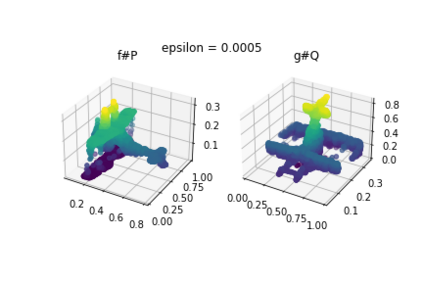
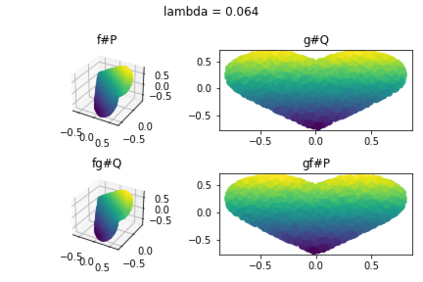
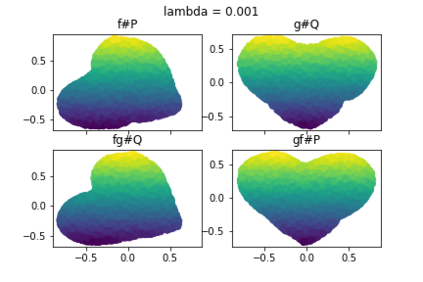
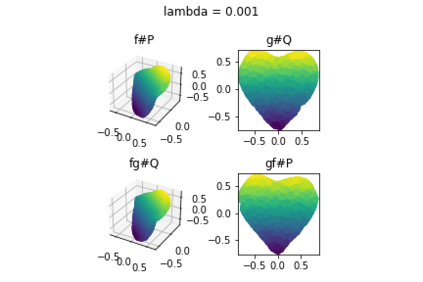
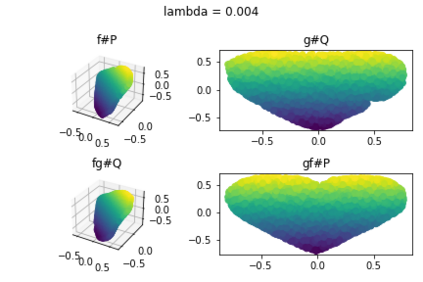
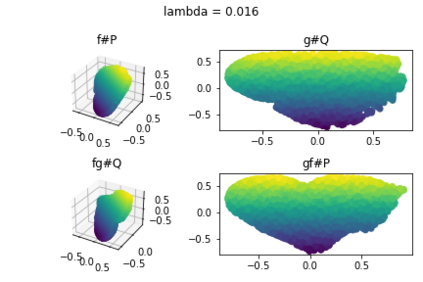
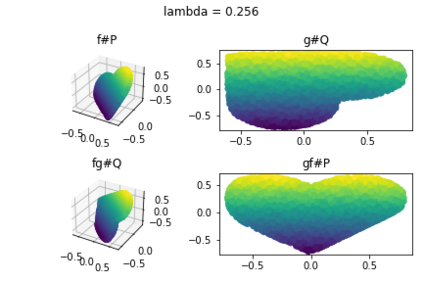
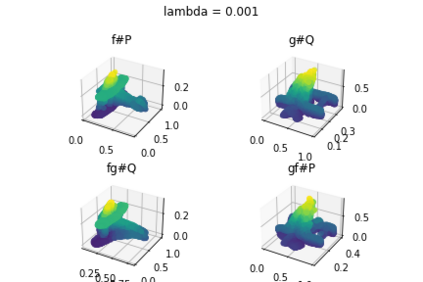
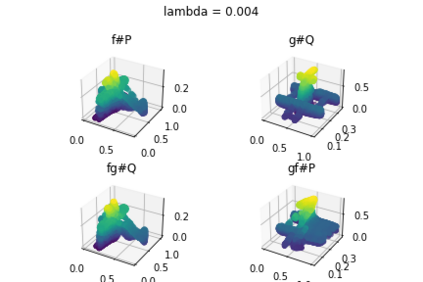
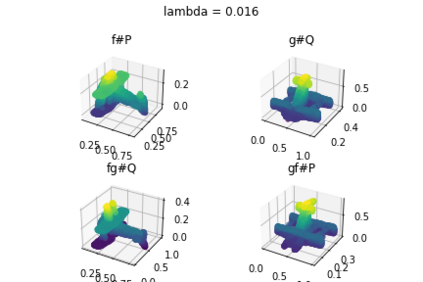
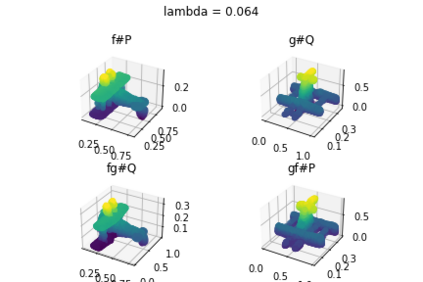
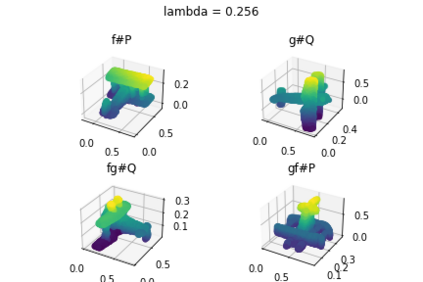
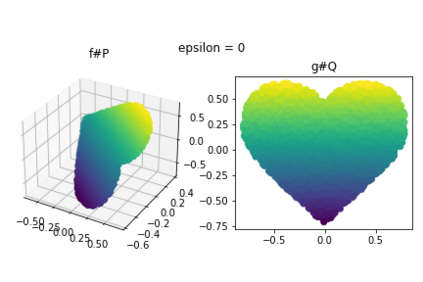
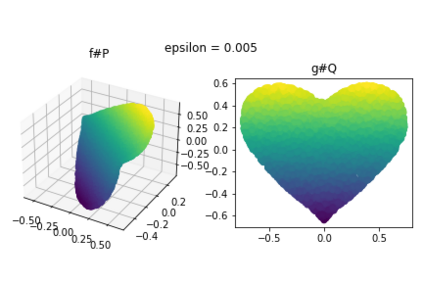
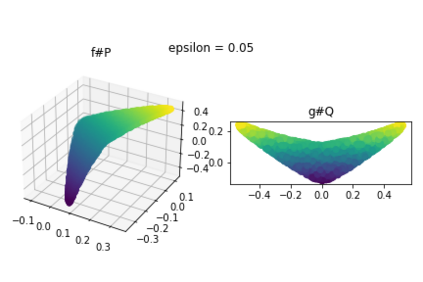
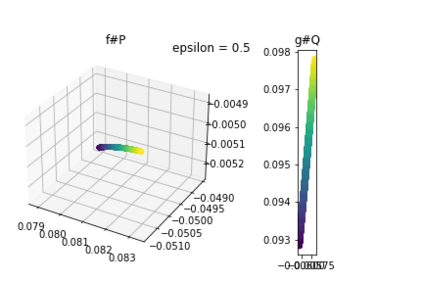
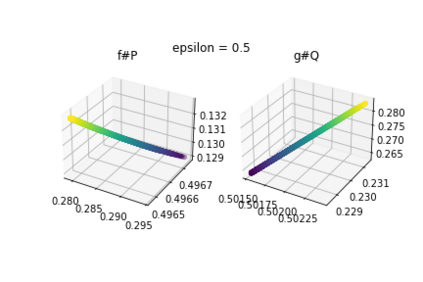
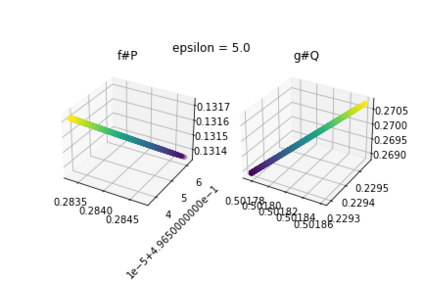
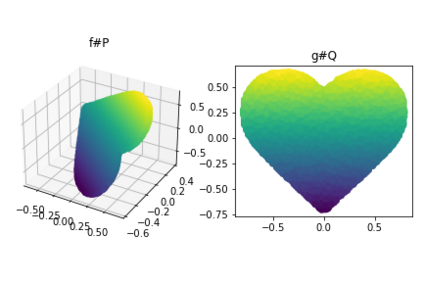
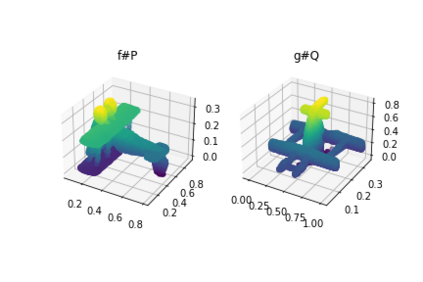
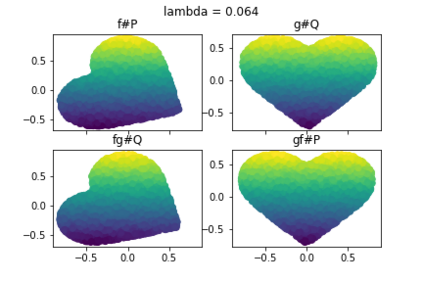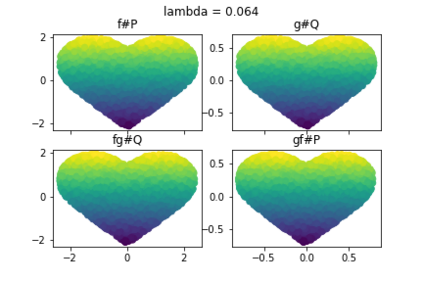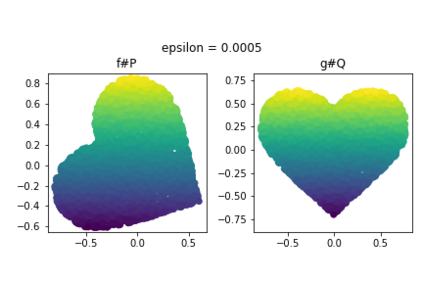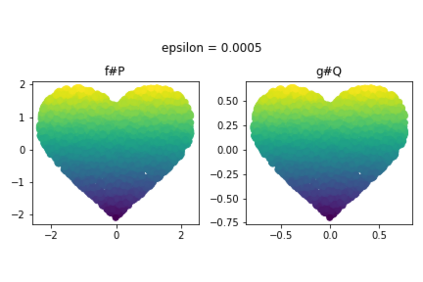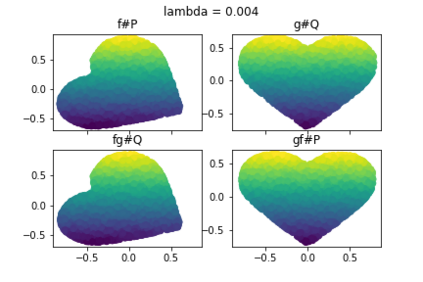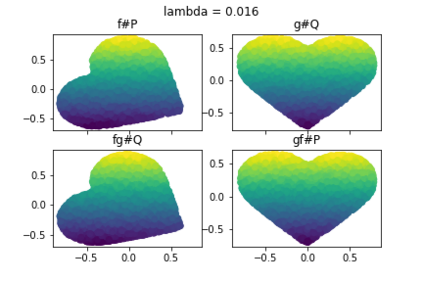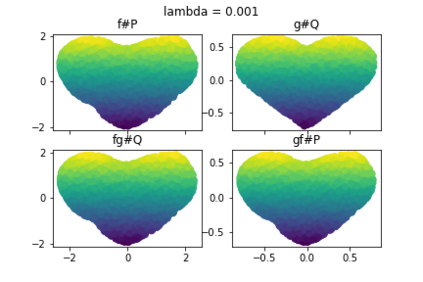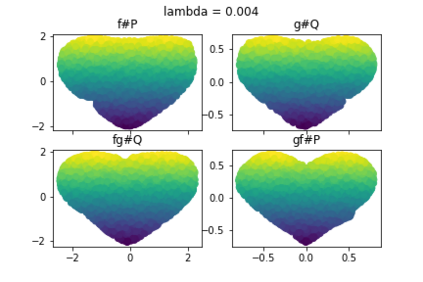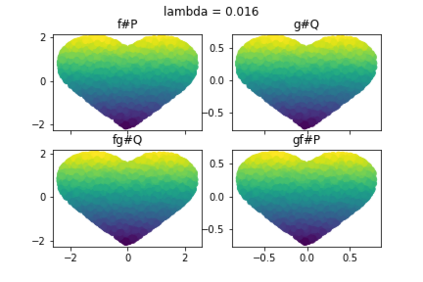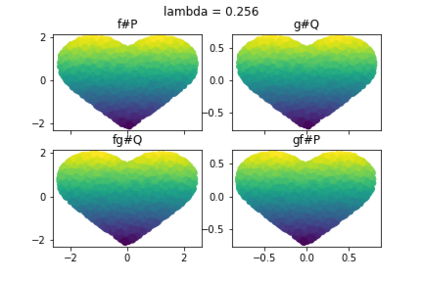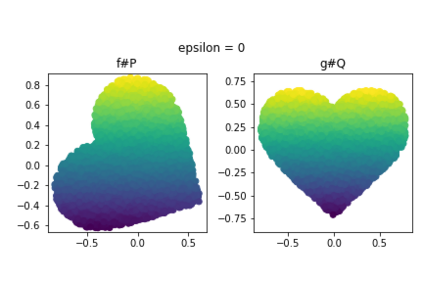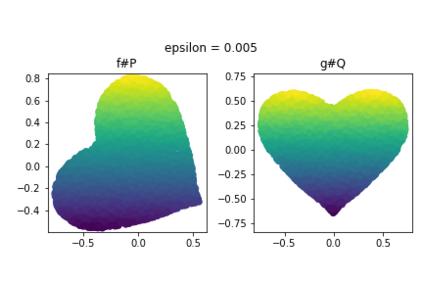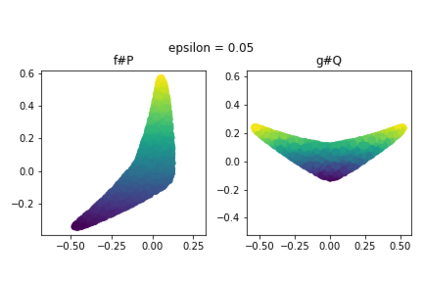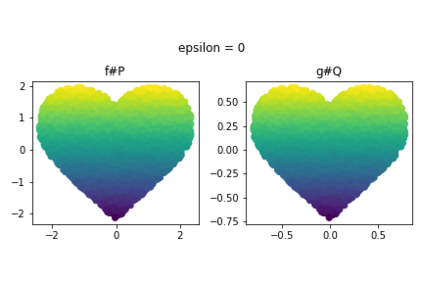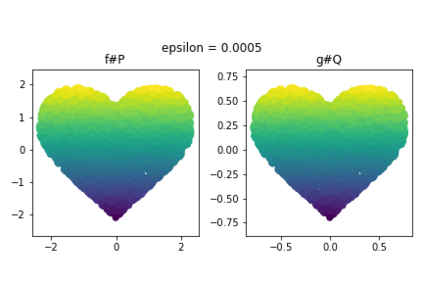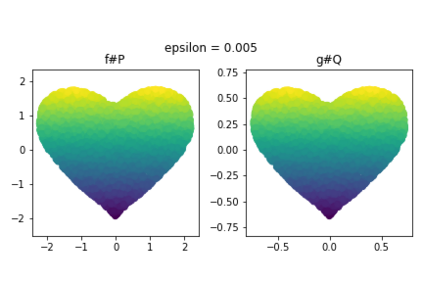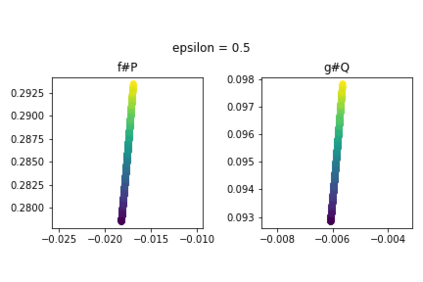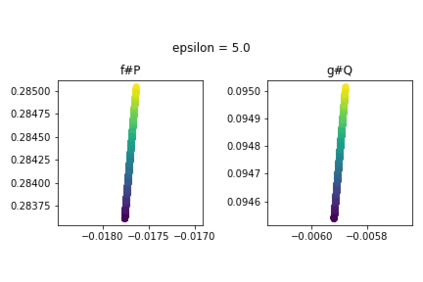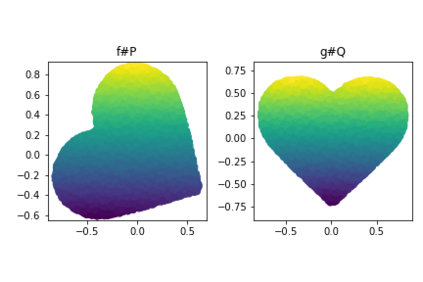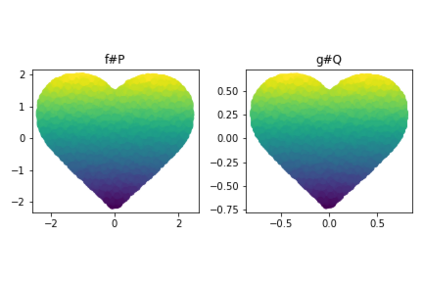Discrepancy measures between probability distributions are at the core of statistical inference and machine learning. In many applications, distributions of interest are supported on different spaces, and yet a meaningful correspondence between data points is desired. Motivated to explicitly encode consistent bidirectional maps into the discrepancy measure, this work proposes a novel unbalanced Monge optimal transport formulation for matching, up to isometries, distributions on different spaces. Our formulation arises as a principled relaxation of the Gromov-Haussdroff distance between metric spaces, and employs two cycle-consistent maps that push forward each distribution onto the other. We study structural properties of the proposed discrepancy and, in particular, show that it captures the popular cycle-consistent generative adversarial network (GAN) framework as a special case, thereby providing the theory to explain it. Motivated by computational efficiency, we then kernelize the discrepancy and restrict the mappings to parametric function classes. The resulting kernelized version is coined the generalized maximum mean discrepancy (GMMD). Convergence rates for empirical estimation of GMMD are studied and experiments to support our theory are provided.
翻译:概率分布的不一致度度是统计推论和机器学习的核心。 在许多应用中, 利益分布在不同空间得到支持, 但希望数据点之间能有一个有意义的对应点。 这项工作旨在将一致的双向分布图明确编码为差异度衡量标准, 并提出了一种新的不平衡的蒙古最优运输配方, 用于匹配, 直至异种, 在不同空间的分布。 我们的配方是作为格罗莫夫- 豪斯德罗夫之间空间间距离的有原则的松动, 并使用两种循环一致的地图, 将每个分布推向另一个。 我们研究了拟议差异的结构性特性, 并特别表明它捕捉了流行的循环一致的基因对抗网络( GAN) 框架, 从而提供了解释它的理论。 受计算效率的驱动, 我们随后将差异集中起来, 并将绘图限制在参数函数等级上。 由此产生的内嵌定的版本是普遍的最大平均值差异( GMD)。 我们研究了对GMD进行实验性估计的趋同率, 并提供了支持我们的理论。