On detecting weak changes in the mean of CHARN models

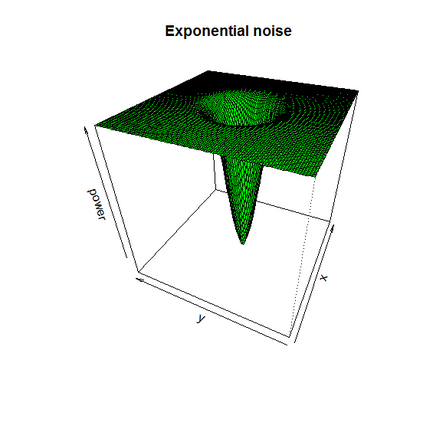
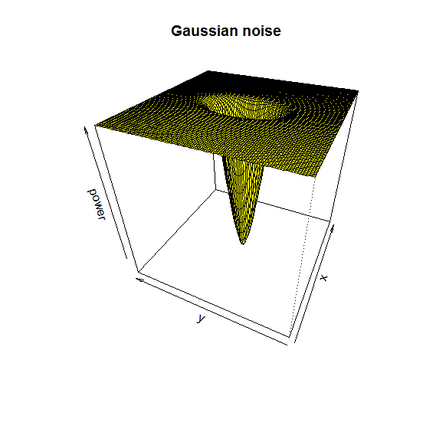
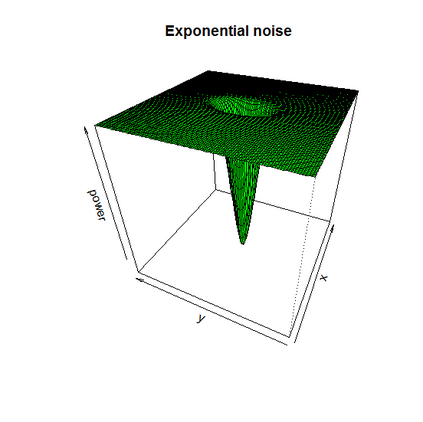
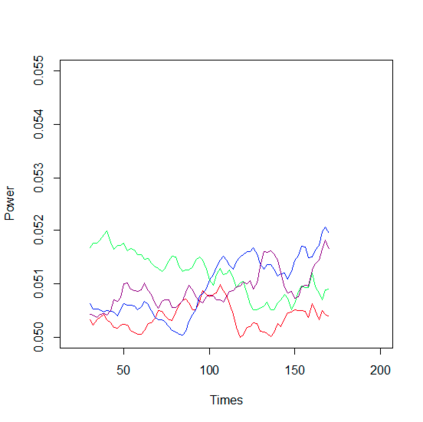
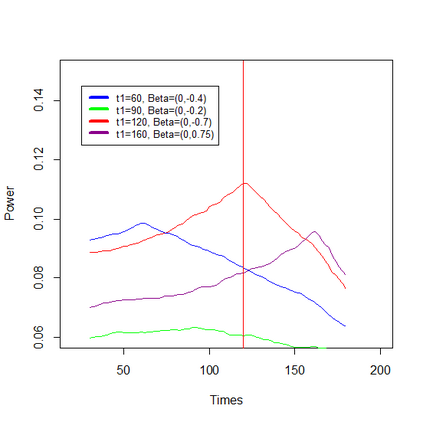
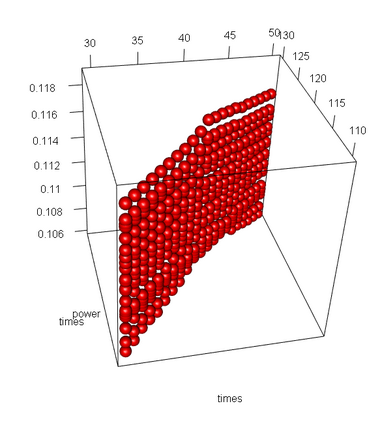
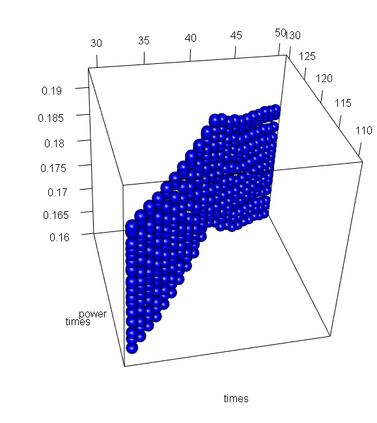
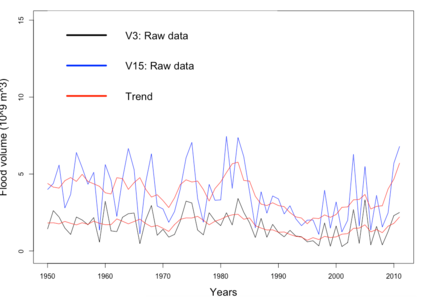
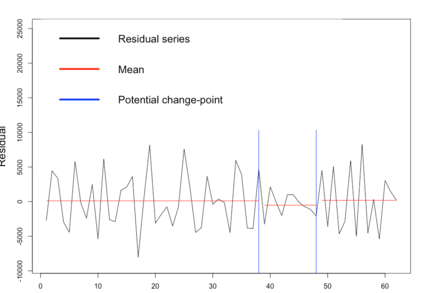
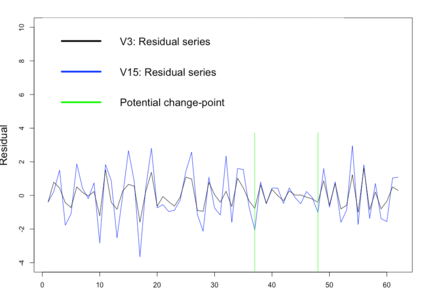
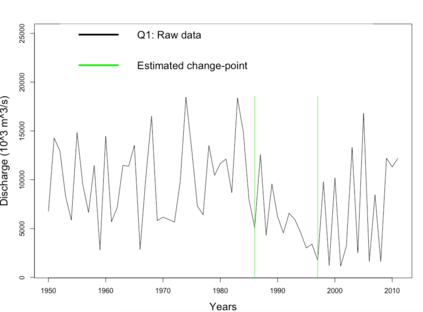
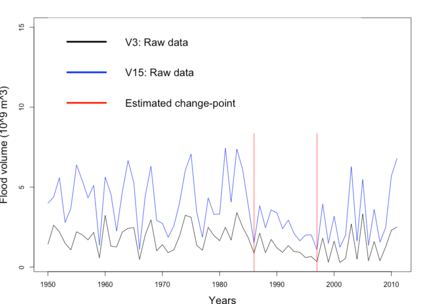
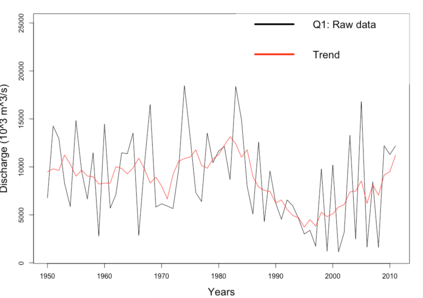
We study a likelihood ratio test for detecting multiple {\it weak} changes in the mean of a class of CHARN models. The locally asymptotically normal (LAN) structure of the family of likelihoods under study is established. It results that the test is asymptotically optimal, and an explicit form of its asymptotic local power is given as a function of candidates change locations and changes magnitudes. Strategies for weak change-points detection and their locations estimates are described. The estimates are obtained as the time indices maximizing an estimate of the local power. A simulation study shows the good performance of our methods compared to some existing approaches. Our results are also applied to three sets of real data.