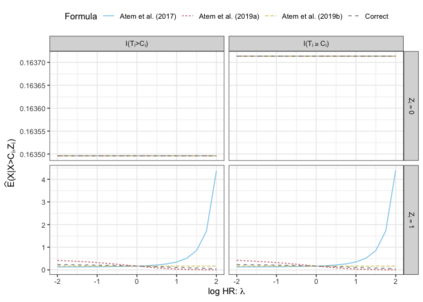
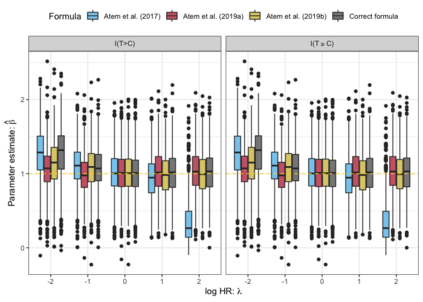
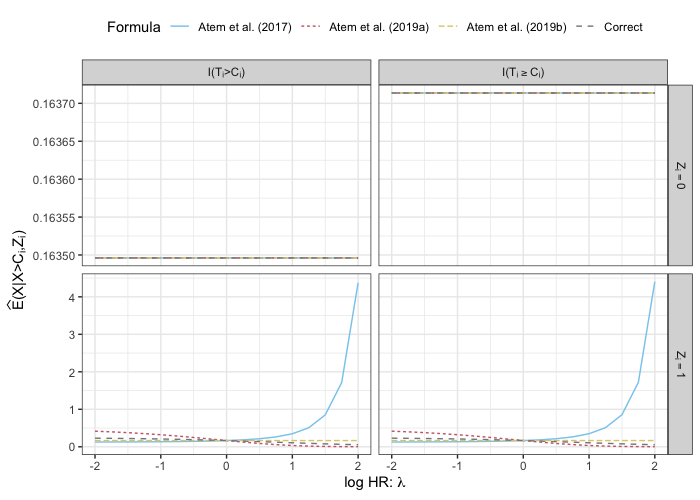
Analysts are often confronted with censoring, wherein some variables are not observed at their true value, but rather at a value that is known to fall above or below that truth. While much attention has been given to the analysis of censored outcomes, contemporary focus has shifted to censored covariates, as well. Missing data is often overcome using multiple imputation, which leverages the entire dataset by replacing missing values with informed placeholders, and this method can be modified for censored data by also incorporating partial information from censored values. One such modification involves replacing censored covariates with their conditional means given other fully observed information, such as the censored value or additional covariates. So-called conditional mean imputation approaches were proposed for censored covariates in Atem et al. [2017], Atem et al.[2019a], and Atem et al. [2019b]. These methods are robust to additional parametric assumptions on the censored covariate and utilize all available data, which is appealing. As we worked to implement these methods, however, we discovered that these three manuscripts provide nonequivalent formulas and, in fact, none is the correct formula for the conditional mean. Herein, we derive the correct form of the conditional mean and demonstrate the impact of the incorrect formulas on the imputed values and statistical inference. Under several settings considered, using an incorrect formula is seen to seriously bias parameter estimation in simple linear regression. Lastly, we provide user-friendly R software, the imputeCensoRd package, to enable future researchers to tackle censored covariates in their data.
翻译:分析者往往面对审查,其中某些变量没有以其真实价值观察到,而是以已知的低于或低于真实价值的价值观察到。虽然对受审查结果的分析给予了很大关注,但当代焦点也转向了受审查的共变。 缺少的数据往往用多种估算方法克服,这种估算方法通过以知情占位符取代缺失的值来利用整个数据集,而这种方法也可以通过纳入受审查值的部分信息来修改受审查数据。这种修改包括以审查值或其他观察到的完整信息,例如审查值或额外共变值,来取代受审查的共变值。在Atem等人(2017年),Atem等人(2019年a)和Atem等人(2019b)中,所谓的有条件平均平均估算法方法为受审查的共变换。这些方法对于受审查的内置值来说是额外的参数假设,而且使用受审查的内置值和使用所有可用数据。我们努力实施这些方法时,我们发现这三份手稿提供了非等值的公式,在事实中,我们用一种有条件的正变的公式来证明。