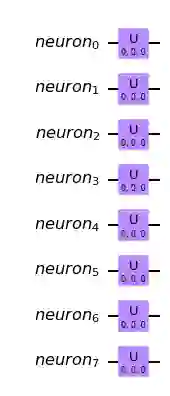
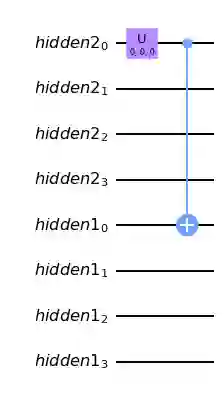
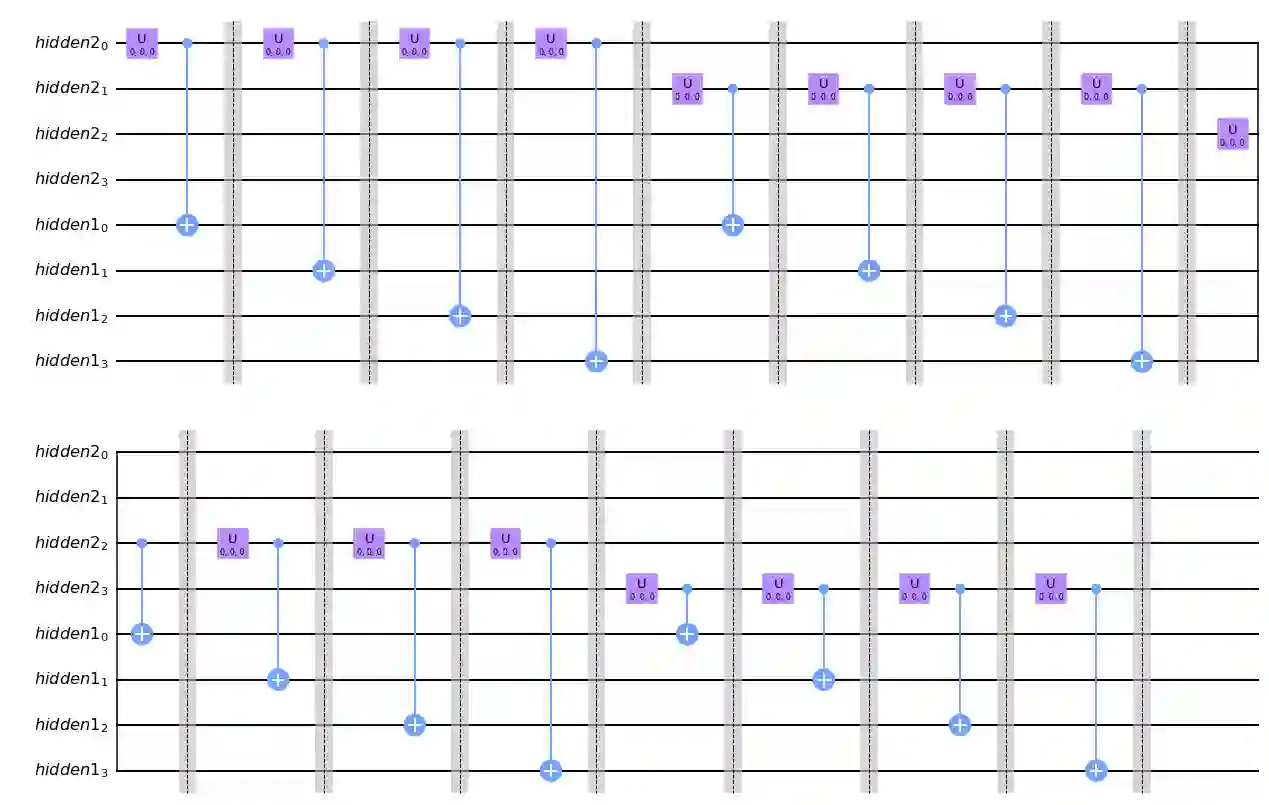
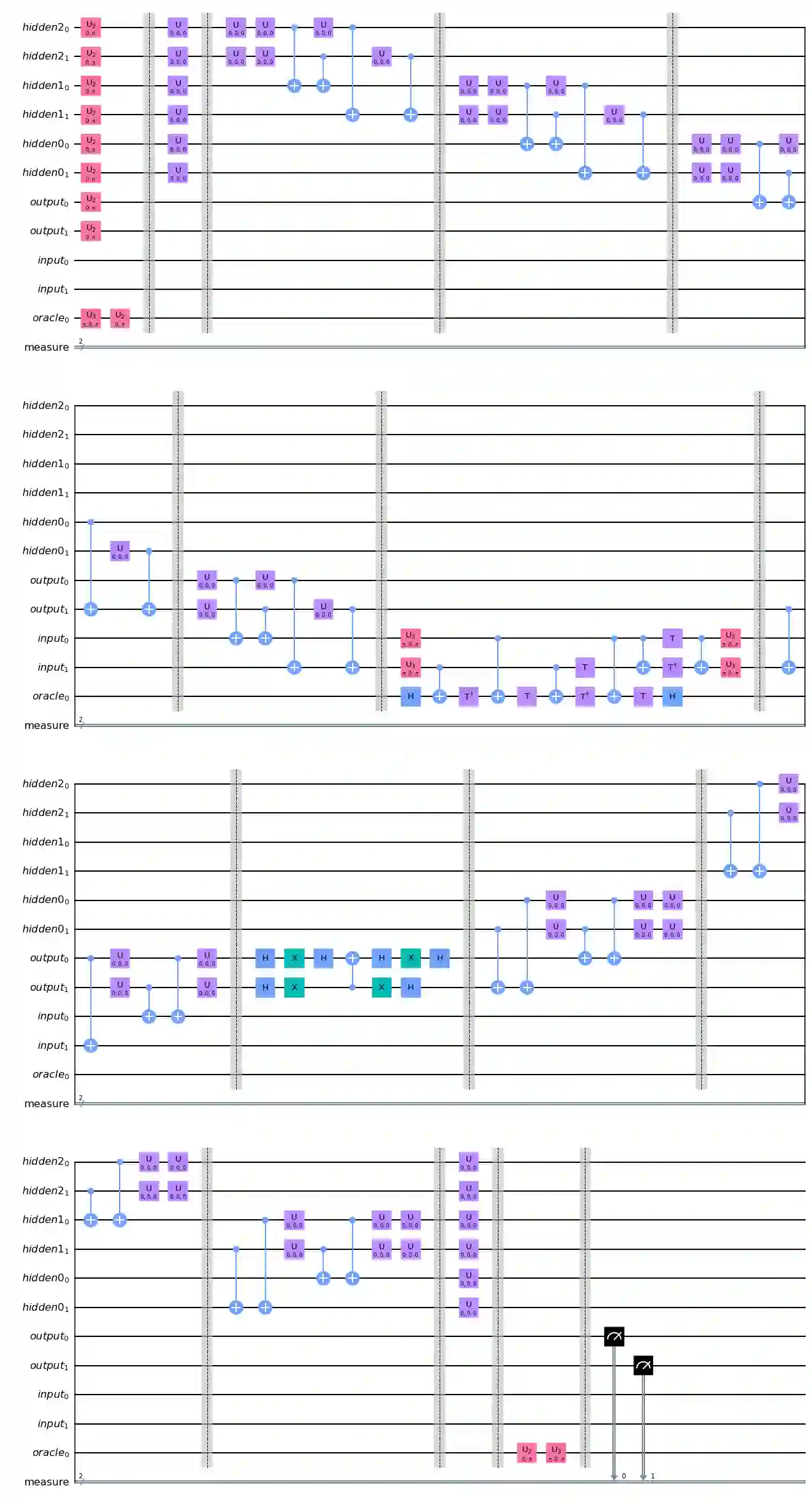
We propose a novel paradigm of integration of Grover's algorithm in a machine learning framework: the inductive Grover oracular quantum neural network (IGO-QNN). The model defines a variational quantum circuit with hidden layers of parameterized quantum neurons densely connected via entangle synapses to encode a dynamic Grover's search oracle that can be trained from a set of database-hit training examples. This widens the range of problem applications of Grover's unstructured search algorithm to include the vast majority of problems lacking analytic descriptions of solution verifiers, allowing for quadratic speed-up in unstructured search for the set of search problems with relationships between input and output spaces that are tractably underivable deductively. This generalization of Grover's oracularization may prove particularly effective in deep reinforcement learning, computer vision, and, more generally, as a feature vector classifier at the top of an existing model.
翻译:我们提出将格罗弗的算法纳入一个机器学习框架的新模式:感性格罗佛或剖面量子神经网络(IGO-QNN) 。 模型定义了一个变化量子电路,其隐蔽的参数性量子神经元层通过缠绕的突触而紧密相连,以编码动态格罗弗的搜索或触法,从一组数据库破坏训练的例子中可以加以培训。 这扩大了格罗弗非结构化搜索算法的问题应用范围,包括绝大多数缺乏解决方案验证器分析描述的问题,允许在无结构的搜索中进行二次加速,以寻找与输入空间和输出空间之间的关系的一组问题,这些关系是很容易无法被分解的。 这种对格罗弗的剖面化在深度增强学习、计算机视觉以及更一般而言作为现有模型顶部的特性矢量分类器可能特别有效。