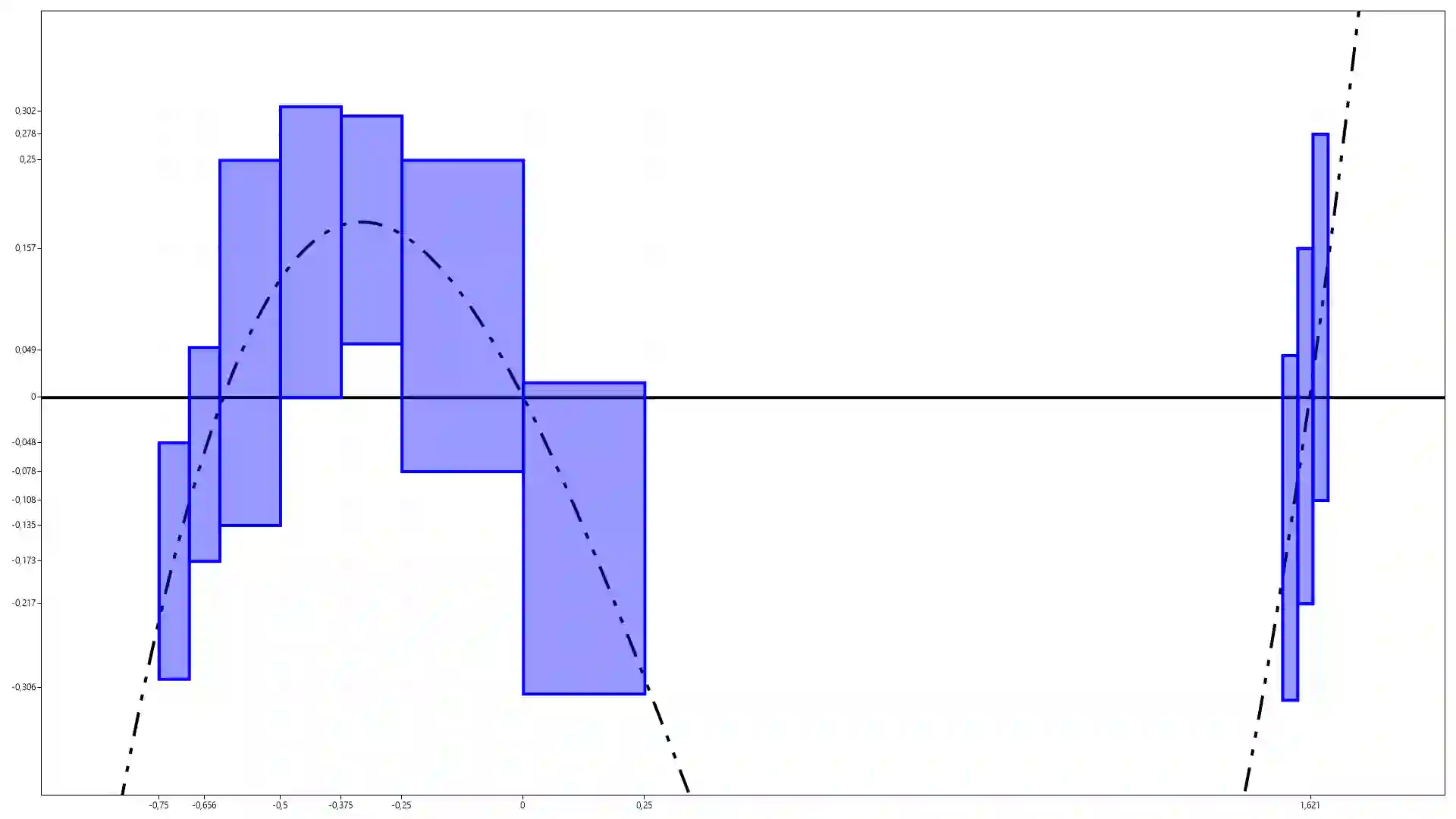
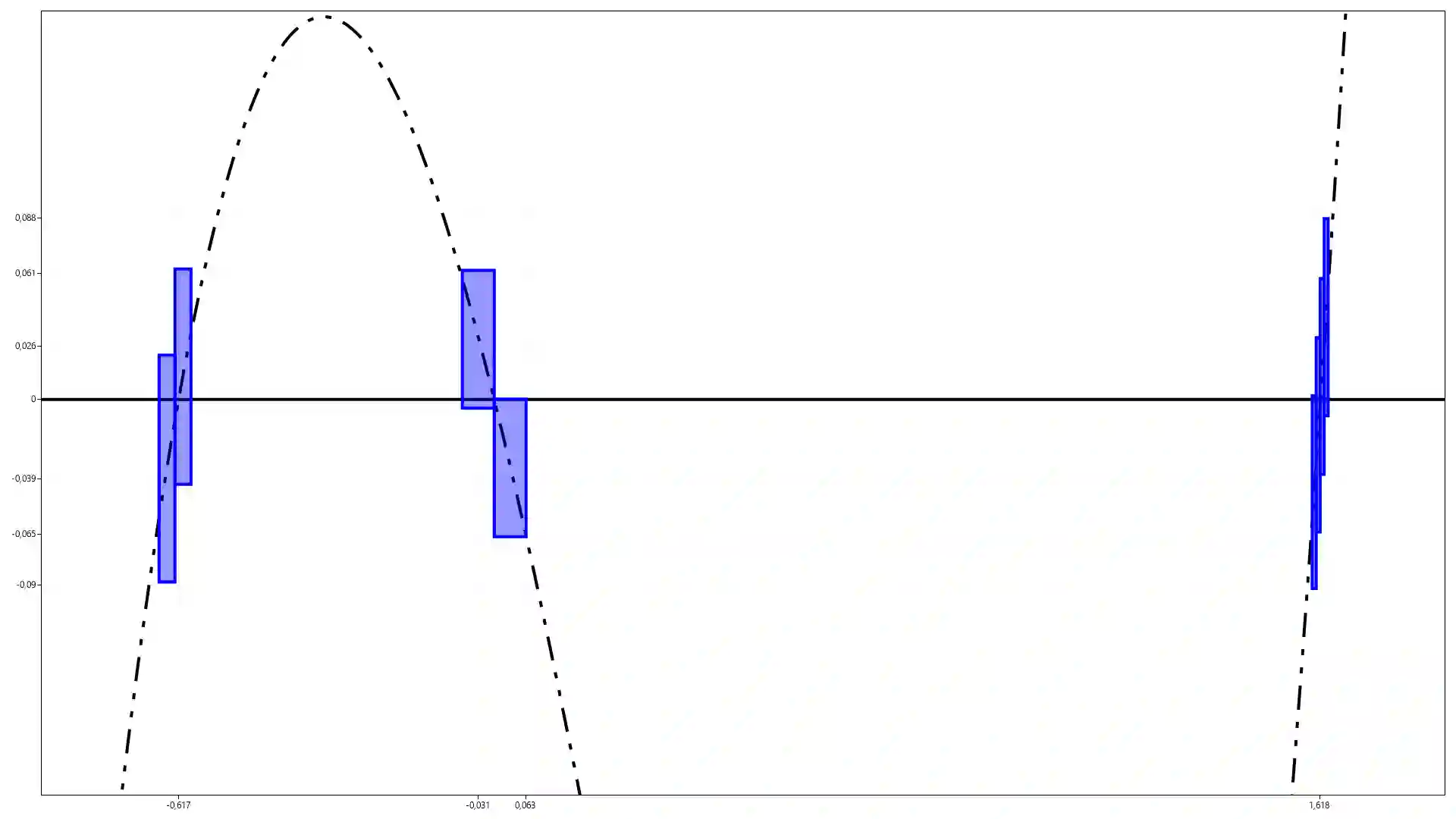
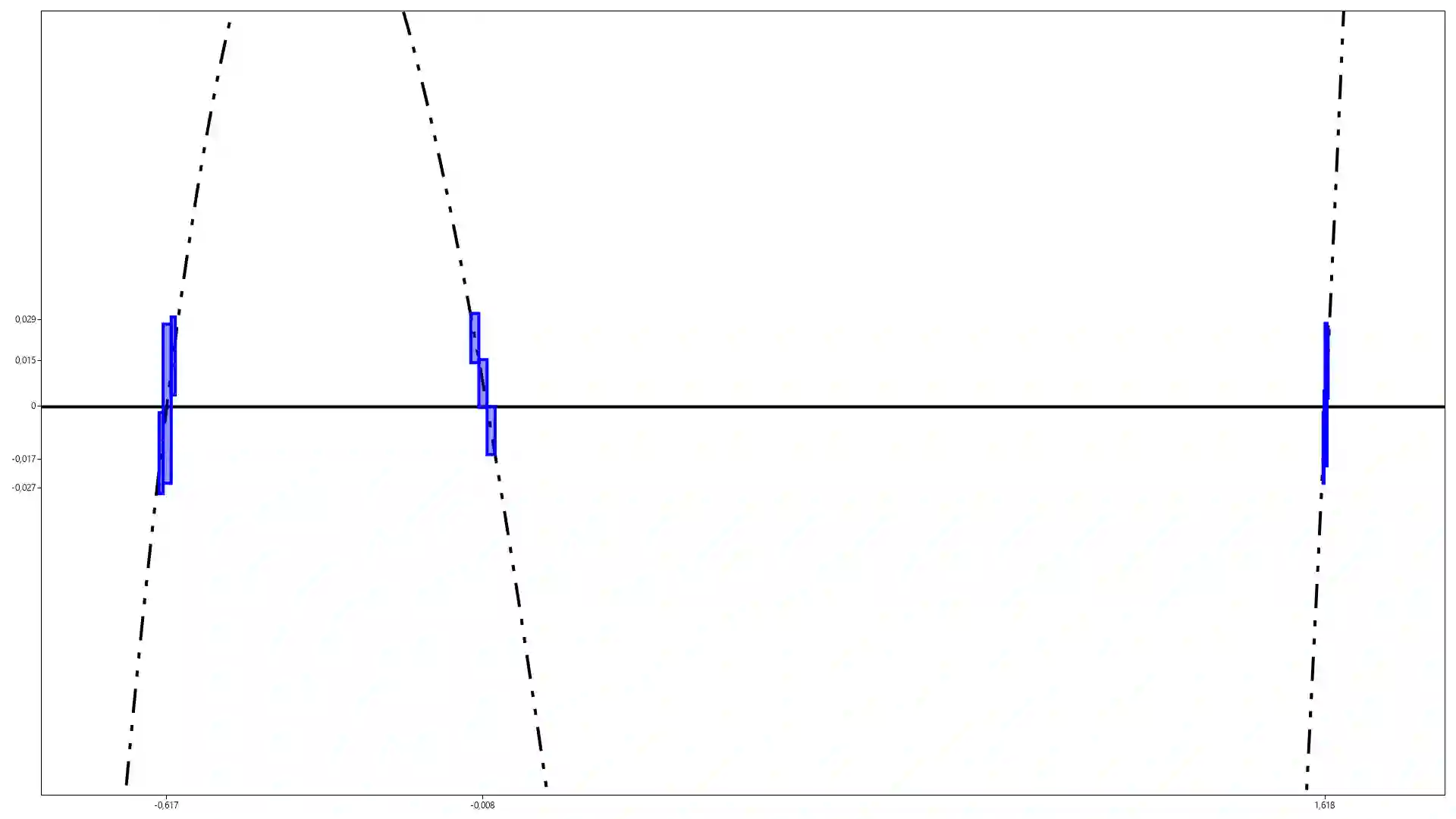
The work is devoted to the construction of a new type of intervals -- functional intervals. These intervals are built on the idea of expanding boundaries from numbers to functions. Functional intervals have shown themselves to be promising for further study and use, since they have more rich algebraic properties compared to classical intervals lamy. In the work, linear functional arithmetic was constructed from one variable. This arithmetic was applied to solve such problems of interval analysis, as minimization of a function on an interval and finding zeros of a function on an interval. Results of numerical experiments for linear functional arithmetic showed a high order of convergence and a higher speed the growth of algorithms when using intervals of a new type, despite the fact that the calculations did not use information about derivative function. Also in the work, a modification of the minimization algorithms functions of several variables, based on the use of the function rational intervals of several variables. As a result, it was Improved speedup of algorithms, but only up to a certain number of unknowns.
翻译:工作用于构建新型的间隔 -- -- 职能间隔。这些间隔建立在从数字到函数的扩大界限的构想基础上。功能间隔表明自己有希望进一步研究和使用,因为与古典间隔相比,它们具有较丰富的代数属性。在工作过程中,从一个变量构建线性功能计算。这种算术用于解决这种间隔分析问题,因为一个间隔的函数最小化,在间隔找到函数零。线性功能算术的数值实验结果显示,在使用新类型的间隔时,算法的趋同程度很高,增长速度更高,尽管计算没有使用衍生函数的信息。此外,在工作过程中,根据若干变量的功能合理间隔,对若干变量的最小化算法函数进行了修改。结果,算法加快了算法的速度,但只达到一定的未知数。