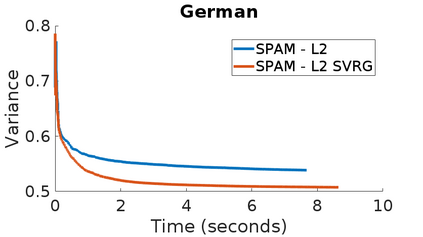
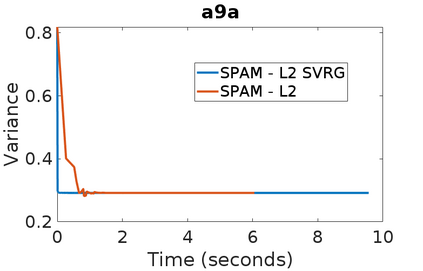
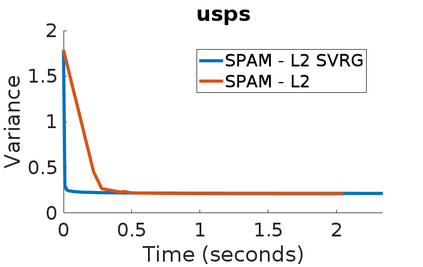
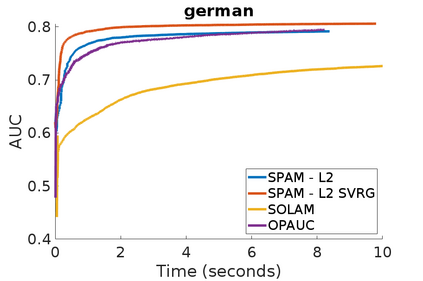
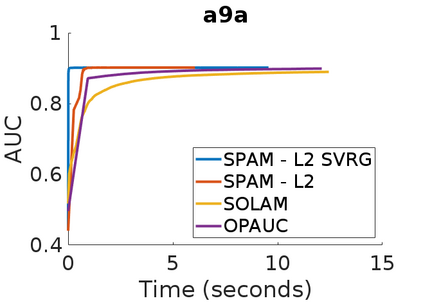
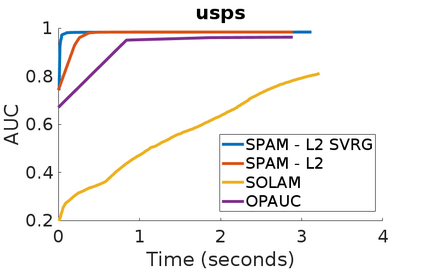
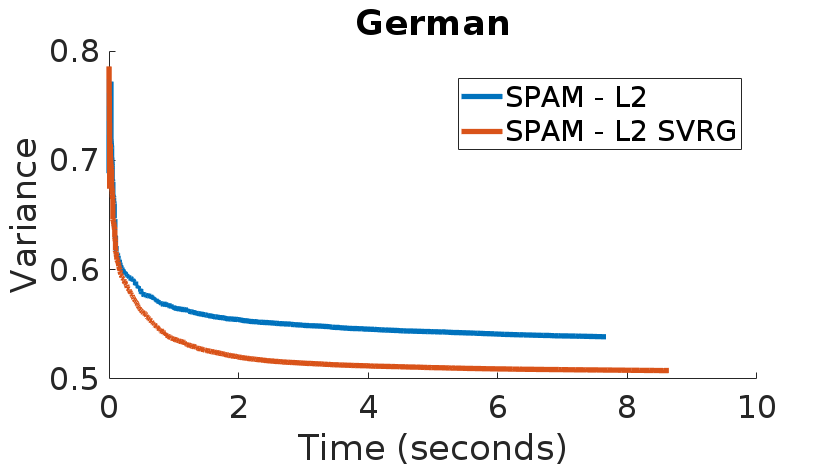
Stochastic Gradient Descent has been widely studied with classification accuracy as a performance measure. However, these stochastic algorithms cannot be directly used when non-decomposable pairwise performance measures are used such as Area under the ROC curve (AUC) which is a common performance metric when the classes are imbalanced. There have been several algorithms proposed for optimizing AUC as a performance metric, and one of the recent being a stochastic proximal gradient algorithm (SPAM). But the downside of the stochastic methods is that they suffer from high variance leading to slower convergence. To combat this issue, several variance reduced methods have been proposed with faster convergence guarantees than vanilla stochastic gradient descent. Again, these variance reduced methods are not directly applicable when non-decomposable performance measures are used. In this paper, we develop a Variance Reduced Stochastic Proximal algorithm for AUC Maximization (\textsc{VRSPAM}) and perform a theoretical analysis as well as empirical analysis to show that our algorithm converges faster than SPAM which is the previous state-of-the-art for the AUC maximization problem.
翻译:然而,当使用非可分解的双向性能衡量尺度时,这些随机算法无法直接使用,例如ROC曲线(AUC)下的区域(AUC),这是在分类不平衡时常见的性能衡量尺度。为了优化AUC作为性能衡量尺度,提出了几种计算法,最近提出的一种算法是随机准度梯度算法(SPAM),但是,这些随机分析法的下方是,它们存在高差异,导致趋同速度放慢。为解决这一问题,提出了几种差异减少的方法,但保证汇合速度快于香草类相向梯度下降。同样,在使用不可分解的性能衡量尺度时,这些差异减少的方法不直接适用。在本文中,我们为AUC最大化(\ textsc{VRSPAM})开发了差异性减少的蒸气准性准值算法,并进行理论分析,以表明我们的算法比SPAM(AMAM)更快,而SPAM是AUC最大化问题以前的状态。