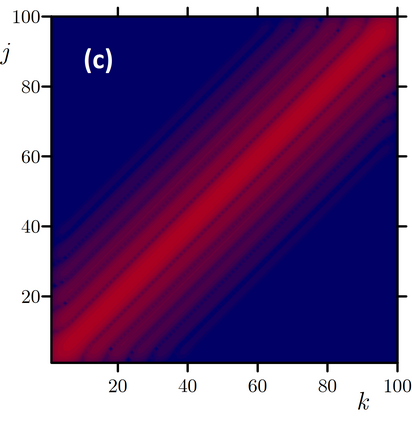
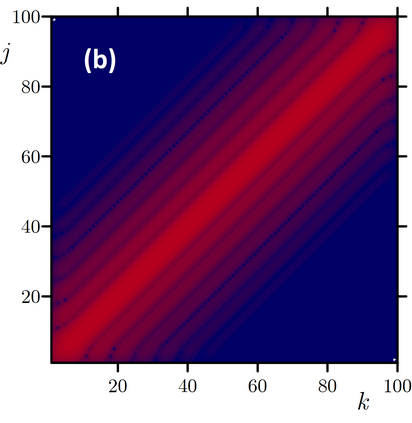
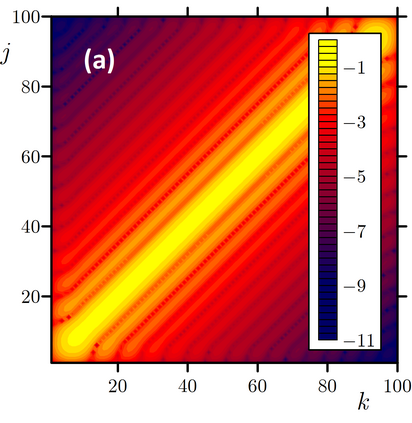
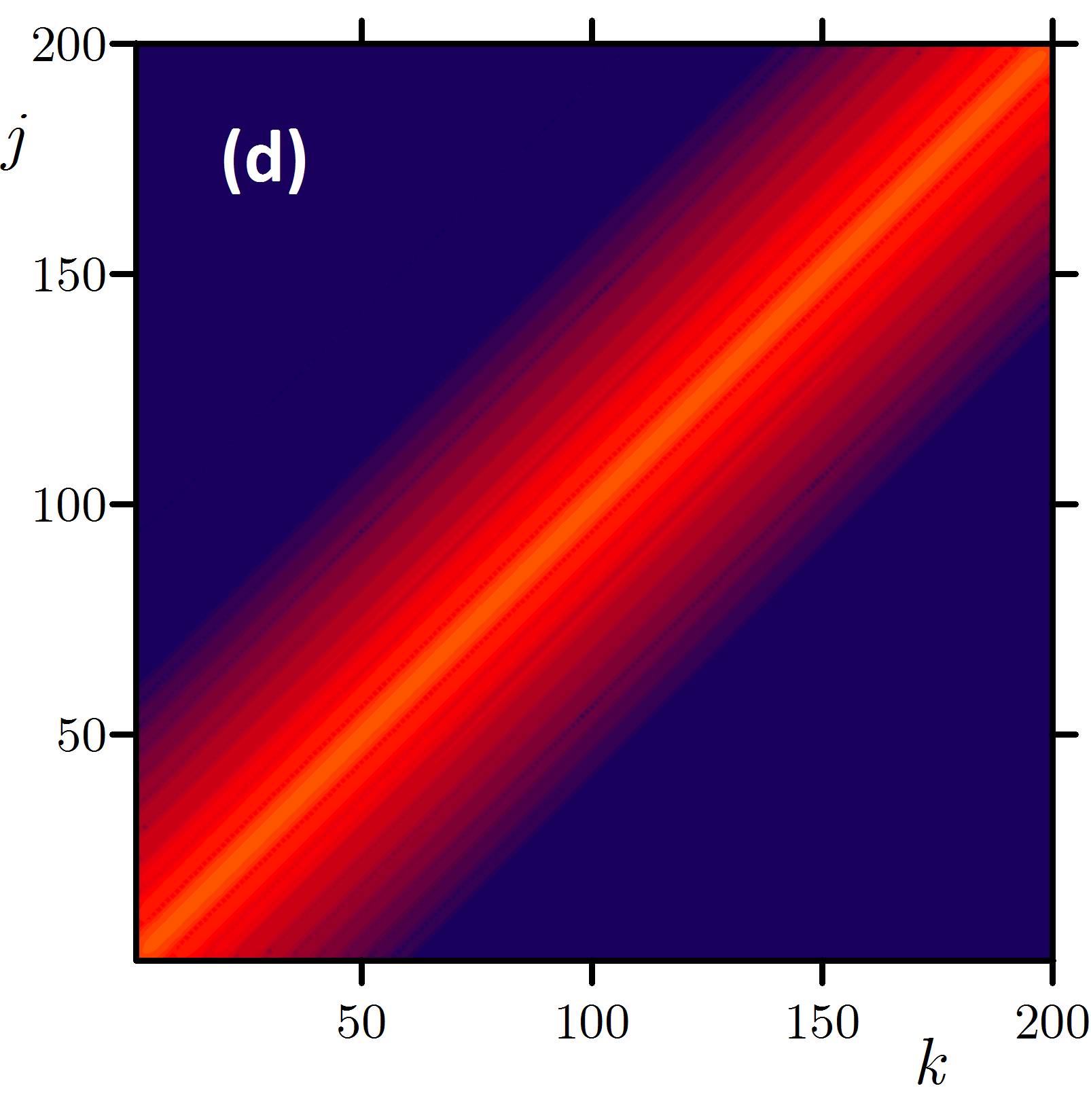
Exponential time differencing methods is a power toll for high-performance numerical simulation of computationally challenging problems in condensed matter and chemical physics, where mathematical models often possess fast oscillating or decaying modes -- in other words, are stiff systems. Practical implementation of these methods for the systems with nondiagonal linear part of equations is exacerbated by infeasibility of an analytical calculation of the exponential of a nondiagonal linear operator; in this case, the coefficients of the exponential time differencing scheme cannot be calculated analytically. We suggest an approach, where these coefficients are numerically calculated with auxiliary problems. We rewrite the high-order Runge--Kutta type schemes in terms of the solutions to these auxiliary problems and practically examine the accuracy and computational performance of these methods for a heterogeneous Cahn--Hilliard equation and a sixth-order spatial derivative equation governing pattern formation in the presence of an additional conservation law.
翻译:指数时间差异法是一种高性能数字模拟精密物质和化学物理学中具有计算挑战性的问题的计算性数字模拟的功率,数学模型往往拥有快速振动或衰变模式 -- -- 换句话说,这些系统是硬系统。用非对角线性方程部分的系统实际实施这些方法,由于无法对非对角线操作员的指数进行分析计算而更加严重;在这种情况下,无法对指数时间差异法的系数进行分析计算。我们建议一种方法,即这些系数是用数字方法计算与辅助问题有关的系数。我们改写这些辅助问题的高级Runge-Kutta型方案,并实际审查这些方法的准确性和计算性,以适应不同Cahn-Hilliard方程和六阶空间衍生方程的公式,在有额外保护法的情况下管理模式的形成。