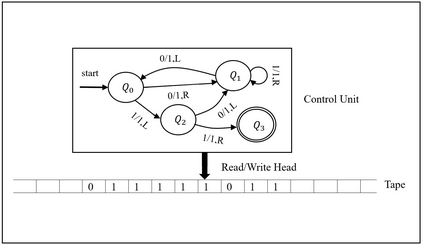
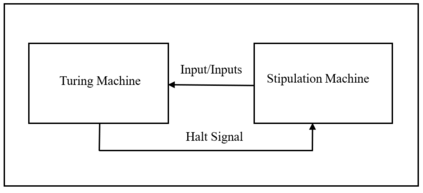
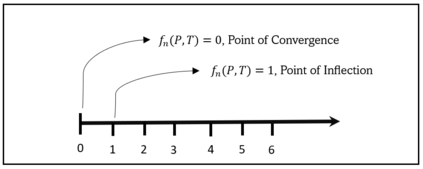
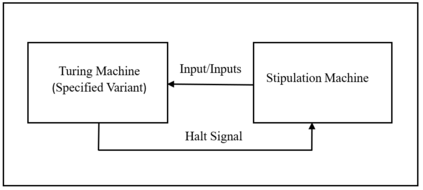
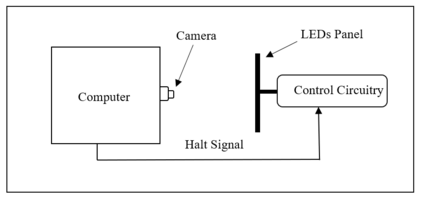
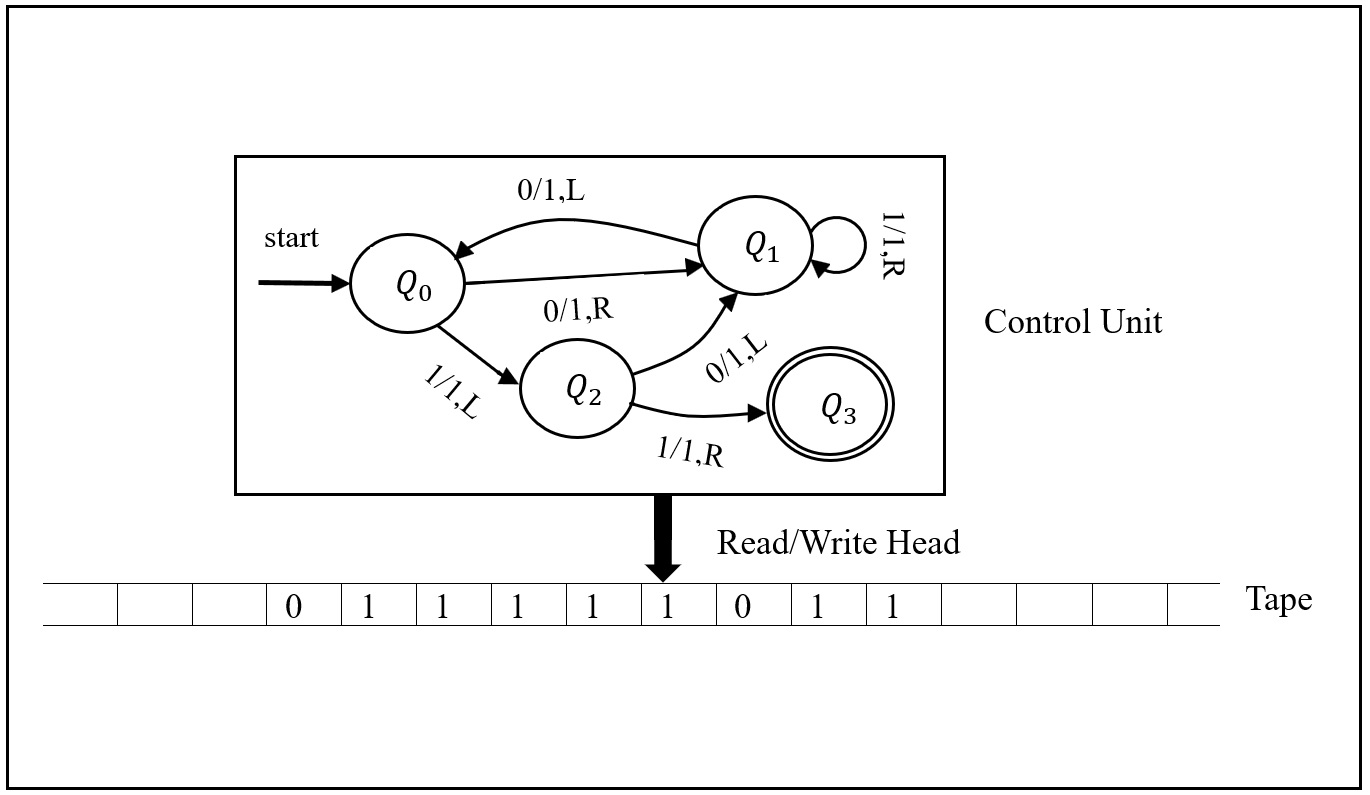
Computational problems are classified into computable and uncomputable problems.If there exists an effective procedure (algorithm) to compute a problem then the problem is computable otherwise it is uncomputable.Turing machines can execute any algorithm therefore every computable problem is Turing computable.There are some variants of Turing machine that appear computationally more powerful but all these variants have been proven equally powerful.The main objective of this work is to revisit and examine the computational power of different variants of Turing machines at very fine-grain level.We achieve this objective by constructing a transform technique for Turing computable problems that transforms computable problems into another type of problems, and then we try to compute the transformed problems through different variants of Turing machine.This paper shows the existence of a realizable computational scheme that can establish a framework to analyze computational characteristics of different variants of Turing machine at infinitesimal scale.
翻译:暂无翻译