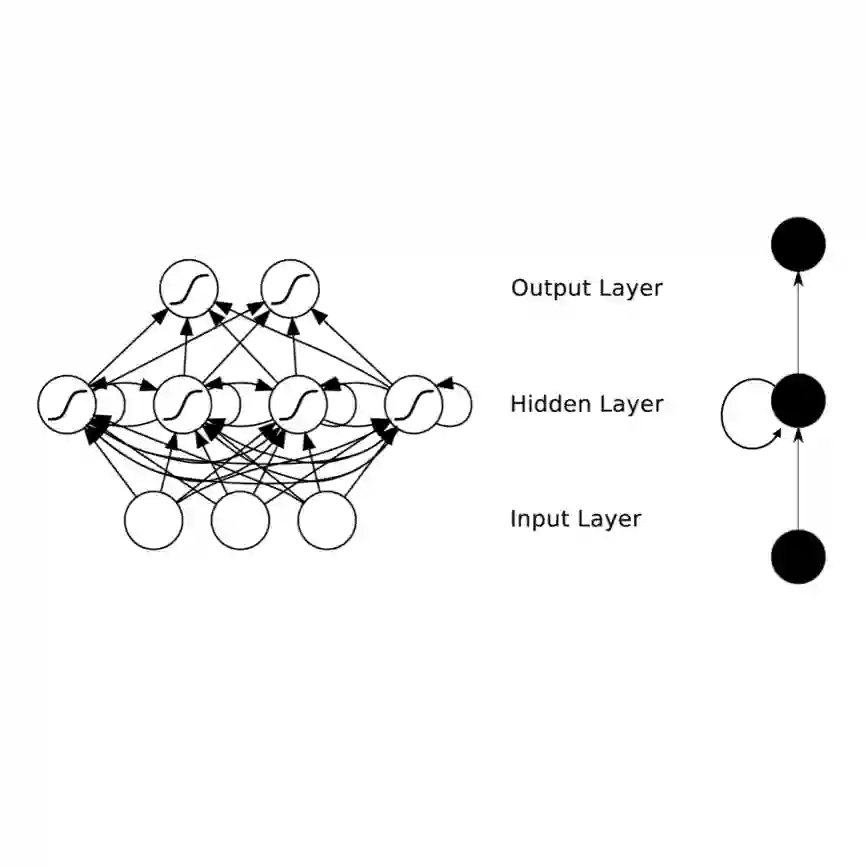
We present the deep neural network multigrid solver (DNN-MG) that we develop for the instationary Navier-Stokes equations. DNN-MG improves computational efficiency using a judicious combination of a geometric multigrid solver and a recurrent neural network with memory. DNN-MG uses the multi-grid method to classically solve on coarse levels while the neural network corrects interpolated solutions on fine ones, thus avoiding the increasingly expensive computations that would have to be performed there. This results in a reduction in computation time through DNN-MG's highly compact neural network. The compactness results from its design for local patches and the available coarse multigrid solutions that provides a "guide" for the corrections. A compact neural network with a small number of parameters also reduces training time and data. Furthermore, the network's locality facilitates generalizability and allows one to use DNN-MG trained on one mesh domain also on different ones. We demonstrate the efficacy of DNN-MG for variations of the 2D laminar flow around an obstacle. For these, our method significantly improves the solutions as well as lift and drag functionals while requiring only about half the computation time of a full multigrid solution. We also show that DNN-MG trained for the configuration with one obstacle can be generalized to other time dependent problems that can be solved efficiently using a geometric multigrid method.
翻译:我们展示了我们为静止导航-斯托克方程式开发的深神经网络多格求解器(DNNN-MG)。DNN-MG使用几何多格求解器和具有记忆的经常性神经网络的明智组合,提高了计算效率。DNNN-MG使用多格方法在粗糙的层次上典型地解决问题,而神经网络则在细微的层次上纠正相互交错的解决办法,从而避免不得不在那里进行的越来越昂贵的计算。这导致通过DNNN-MG高度紧凑的神经网络缩短计算时间。DNNMG设计当地补丁和为校正提供“引导”的现有粗微多格解决方案所产生的紧凑性结果提高了计算效率。一个具有少量参数的紧凑性神经网络也减少了培训时间和数据。此外,网络的地理位置便利了一般化,并允许人们使用在一个网域域上受过训练的DNNGMG计算方法。我们展示了D-MG在障碍周围变化的计算效率。在这方面,我们的方法可以大大改进功能性方法,同时将DGMG的模型作为完整的计算方法,我们所需要的半解算。