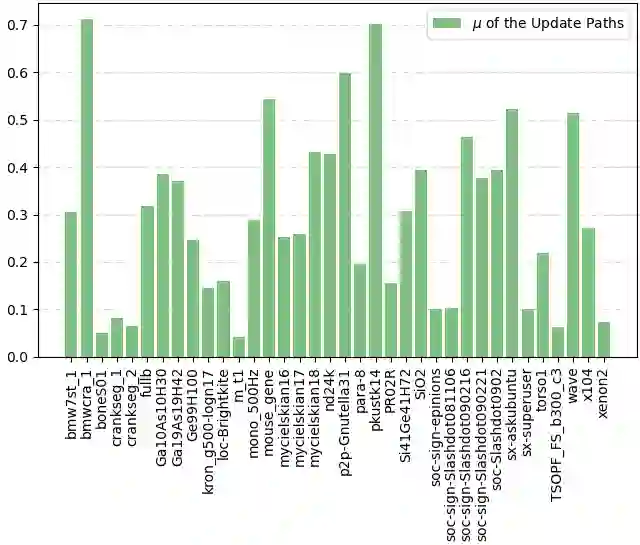
The shortest path problem is a typical problem in graph theory with wide potential applications. The state-of-the-art single-source shortest paths algorithm on the weight graph is the $\Delta$-stepping algorithm, which can efficiently process weighted graphs in parallel. DAWN is an algorithm that addresses the shortest path problem on unweighted graphs, and we propose a weighted version that can handle graphs with weights edges, while maintaining the high scalability and parallelism features as DAWN. The novel version requires $O(\mu m)$ and $O(\mu \cdot E_{wcc})$ times on the connected and unconnected graphs for SSSP problems, respectively. $E_{wcc}$ denote the number of edges included in the largest weakly connected component, and $\mu$ is a constant denoting the average number of path transformations in the tasks. We tested the weighted version on the real graphs from Stanford Network Analysis Platform and SuiteSparse Matrix Collection, which outperformed the solution of $\Delta$-stepping algorithm from Gunrock, achieving a speedup of 43.163$\times$.
翻译:暂无翻译