Multi-Marginal Gromov-Wasserstein Transport and Barycenters

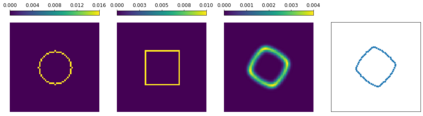
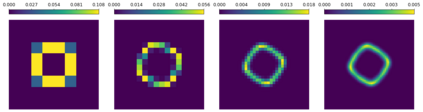
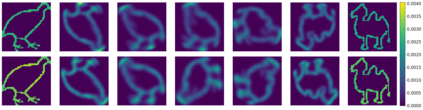
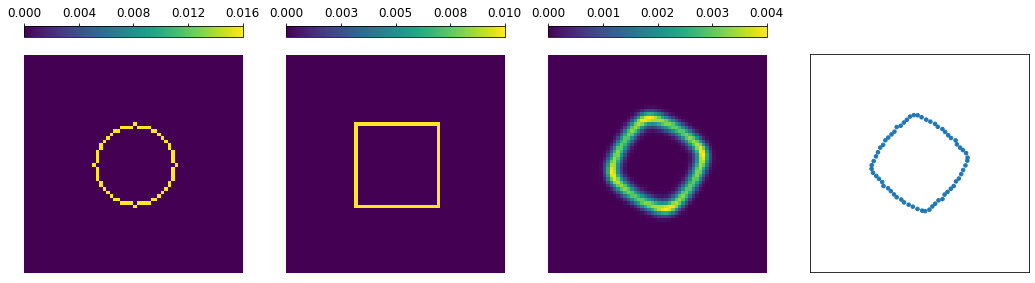
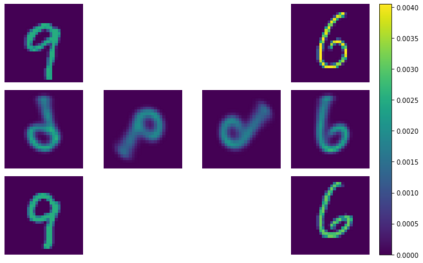Gromov-Wasserstein (GW) distances are generalizations of Gromov-Haussdorff and Wasserstein distances. Due to their invariance under certain distance-preserving transformations they are well suited for many practical applications. In this paper, we introduce a concept of multi-marginal GW transport as well as its regularized and unbalanced versions. Then we generalize a bi-convex relaxation of the GW transport to our multi-marginal setting which is tight if the cost function is conditionally negative definite in a certain sense. The minimization of this relaxed model can be done by an alternating algorithm, where each step can be performed by a Sinkhorn scheme for a multi-marginal transport problem. We show a relation of our multi-marginal GW problem for a tree-structured cost function to an (unbalanced) GW barycenter problem and present different proof-of-concept numerical results.