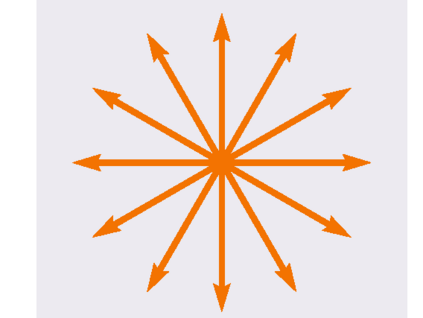
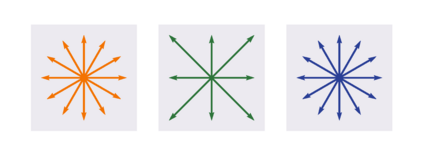
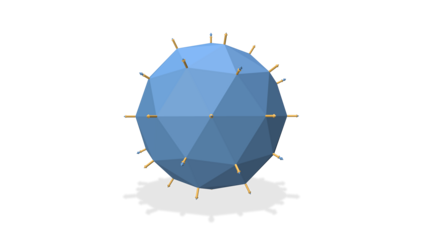
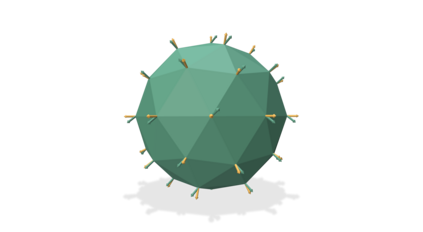
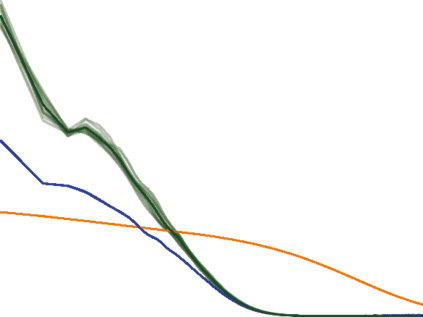
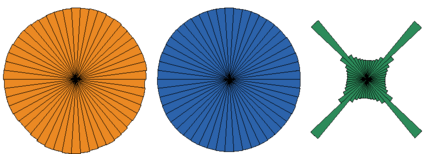
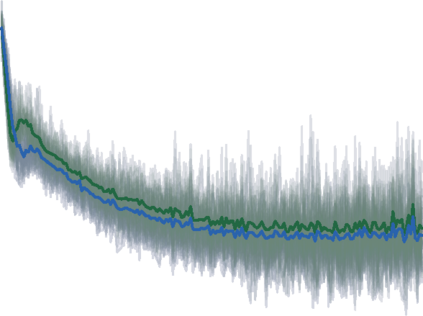
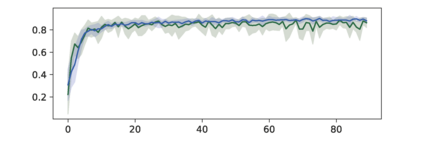
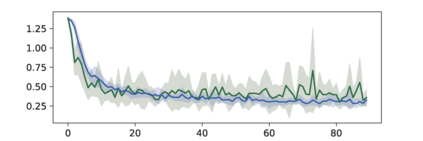
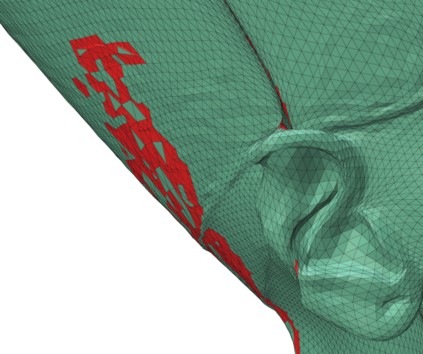
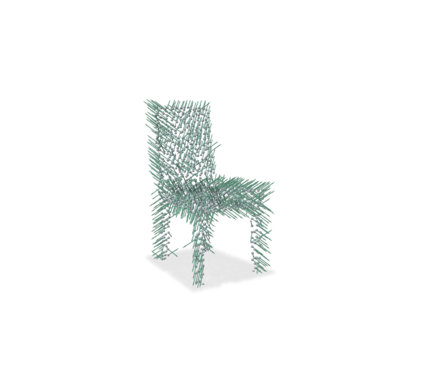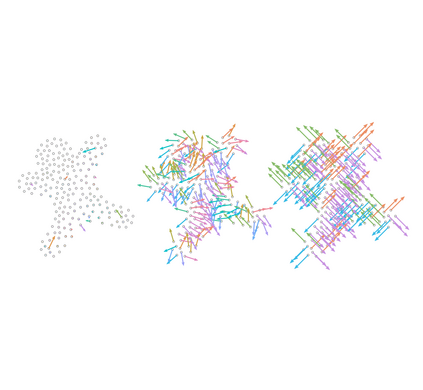The Adam optimization algorithm has proven remarkably effective for optimization problems across machine learning and even traditional tasks in geometry processing. At the same time, the development of equivariant methods, which preserve their output under the action of rotation or some other transformation, has proven to be important for geometry problems across these domains. In this work, we observe that Adam $-$ when treated as a function that maps initial conditions to optimized results $-$ is not rotation equivariant for vector-valued parameters due to per-coordinate moment updates. This leads to significant artifacts and biases in practice. We propose to resolve this deficiency with VectorAdam, a simple modification which makes Adam rotation-equivariant by accounting for the vector structure of optimization variables. We demonstrate this approach on problems in machine learning and traditional geometric optimization, showing that equivariant VectorAdam resolves the artifacts and biases of traditional Adam when applied to vector-valued data, with equivalent or even improved rates of convergence.
翻译:亚当优化算法被证明非常有效地优化了各种机器学习甚至传统的几何处理任务之间的优化问题。 同时,开发等式方法,在轮换或某些其他转换的行动下保留其输出,已证明对这些领域的几何问题很重要。 在这项工作中,我们观察到,当亚当作为一个函数来绘制优化结果的初步条件时,当用美元来绘制最佳结果的初始条件时,当用美元来绘制时,它并不是矢量值值参数的旋转等式,因为每坐标时刻更新。这会导致大量文物和实践中的偏差。我们提议用VictorAdam来解决这一缺陷。VictorAdam是一种简单的修改,它使Adam通过计算优化变量的矢量结构而实现旋转和等同。我们在机器学习和传统几何优化方面的问题上展示了这一方法,表明等式矢量值Adam在将传统亚当的文物和偏差应用到矢量值数据时,其趋同甚至改进了趋同率。