Computability of magnetic Schrödinger and Hartree equations on unbounded domains

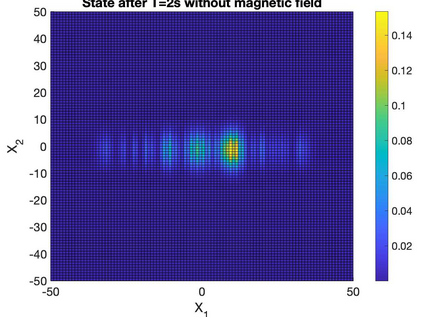
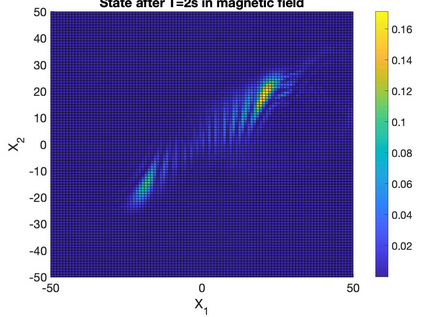
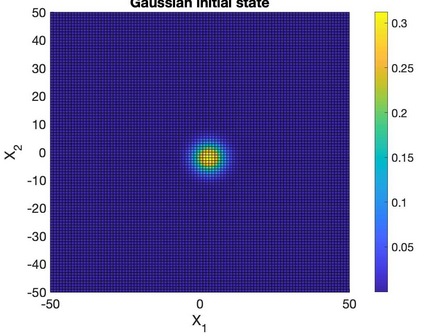
We study the computability of global solutions to linear Schr\"odinger equations with magnetic fields and the Hartree equation on $\mathbb R^3$. We show that the solution can always be globally computed with error control on the entire space if there exist a priori decay estimates in generalized Sobolev norms on the initial state. Using weighted Sobolev norm estimates, we show that the solution can be computed with uniform computational runtime with respect to initial states and potentials.