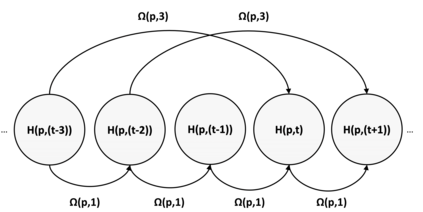
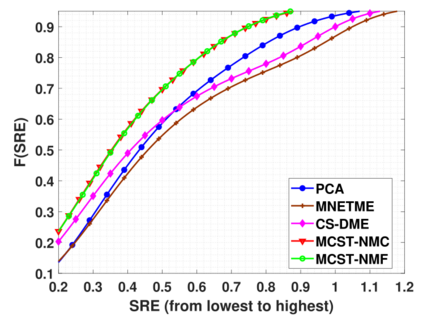
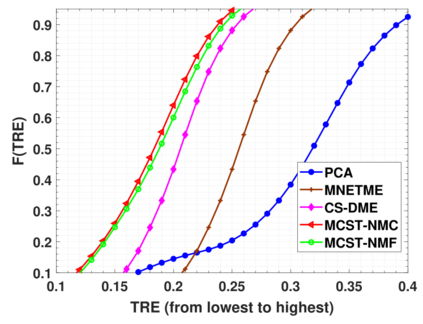
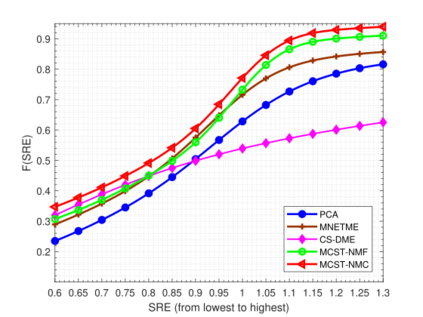
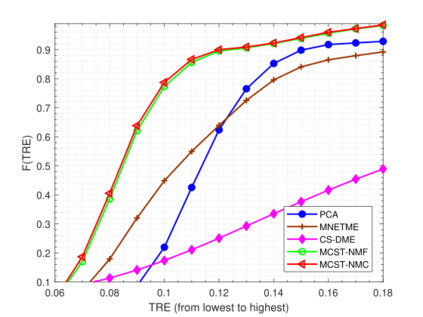
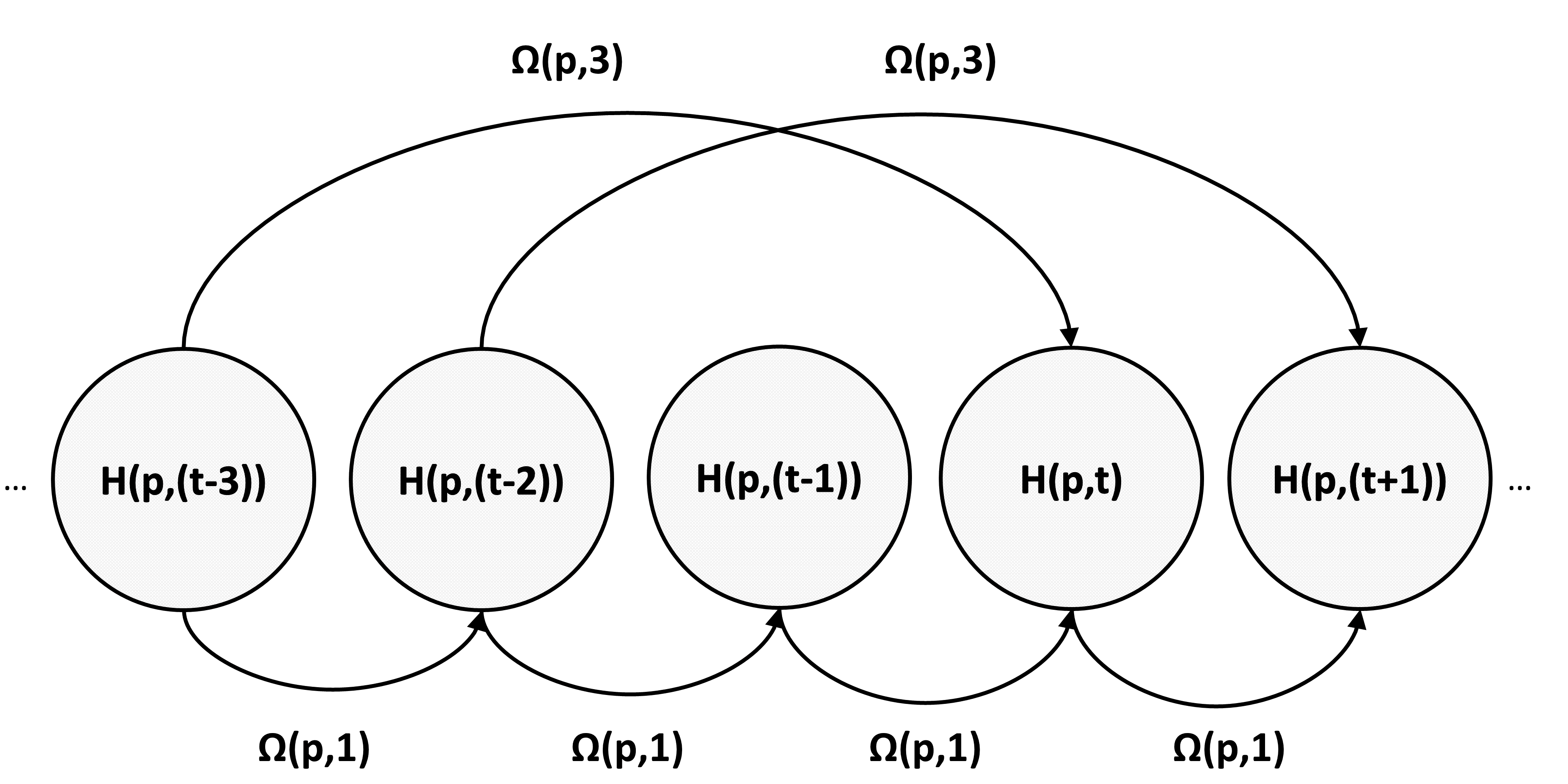
Network traffic matrix estimation is an ill-posed linear inverse problem: it requires to estimate the unobservable origin destination traffic flows, X, given the observable link traffic flows, Y, and a binary routing matrix, A, which are such that Y = AX. This is a challenging but vital problem as accurate estimation of OD flows is required for several network management tasks. In this paper, we propose a novel model for the network traffic matrix estimation problem which maps high-dimension OD flows to low-dimension latent flows with the following three constraints: (1) nonnegativity constraint on the estimated OD flows, (2) autoregression constraint that enables the proposed model to effectively capture temporal patterns of the OD flows, and (3) orthogonality constraint that ensures the mapping between low-dimensional latent flows and the corresponding link flows to be distance preserving. The parameters of the proposed model are estimated with a training algorithm based on Nesterov accelerated gradient and generally shows fast convergence. We validate the proposed traffic flow estimation model on two real backbone IP network datasets, namely Internet2 and G'EANT. Empirical results show that the proposed model outperforms the state-of-the-art models not only in terms of tracking the individual OD flows but also in terms of standard performance metrics. The proposed model is also found to be highly scalable compared to the existing state-of-the-art approaches.
翻译:网络流量矩阵估计是一个不测的线性反向问题:它要求估计不可观察的目的地交通流量,X,考虑到观测到的交通流量链接,Y,以及一个二进路路路母矩阵,A,即Y=AX。这是一个具有挑战性但至关重要的问题,因为需要为若干网络管理任务准确估计OD流量。在本文中,我们提出了网络交通流量矩阵估计问题的新模式,其中绘制了向低分散潜流的高差异OD流动分布图,并有以下三个限制:(1) 对估计的OD流量的不惯性限制,X,Y和二进路路路路径矩阵,A,即Y=A。这是一个具有挑战性但又至关重要的问题,因为对于低度潜在流动和相应链接流量的准确估计,对于若干网络管理任务是必要的。我们用基于Nesterov加速梯度和一般显示快速趋同性的培训算法来估计拟议中的模型。我们验证了两个真正的主干线IP网络数据集的拟议流量估算模型,即互联网2和GEANT的流量限制,(2)自反向自流限制,使拟议的模型能够有效捕捉捉到OD流动,而仅按现有标准格式的模型的运行模式,也显示了拟议的单个模式。