Curiosity Killed or Incapacitated the Cat and the Asymptotically Optimal Agent

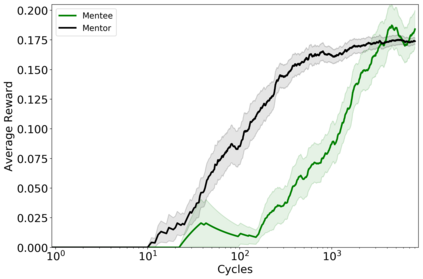
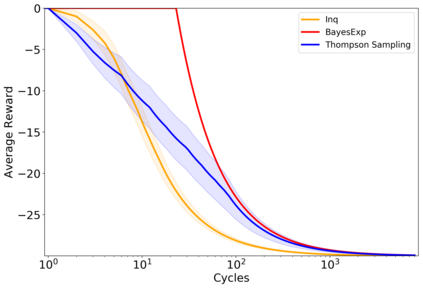
Reinforcement learners are agents that learn to pick actions that lead to high reward. Ideally, the value of a reinforcement learner's policy approaches optimality--where the optimal informed policy is the one which maximizes reward. Unfortunately, we show that if an agent is guaranteed to be "asymptotically optimal" in any (stochastically computable) environment, then subject to an assumption about the true environment, this agent will be either "destroyed" or "incapacitated" with probability 1. Much work in reinforcement learning uses an ergodicity assumption to avoid this problem. Often, doing theoretical research under simplifying assumptions prepares us to provide practical solutions even in the absence of those assumptions, but the ergodicity assumption in reinforcement learning may have led us entirely astray in preparing safe and effective exploration strategies for agents in dangerous environments. Rather than assuming away the problem, we present an agent, Mentee, with the modest guarantee of approaching the performance of a mentor, doing safe exploration instead of reckless exploration. Critically, Mentee's exploration probability depends on the expected information gain from exploring. In a simple non-ergodic environment with a weak mentor, we find Mentee outperforms existing asymptotically optimal agents and its mentor.