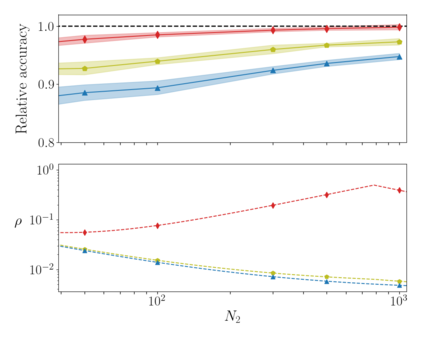
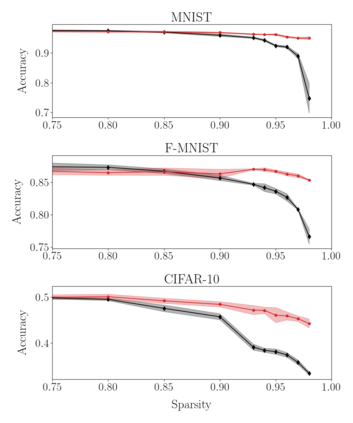
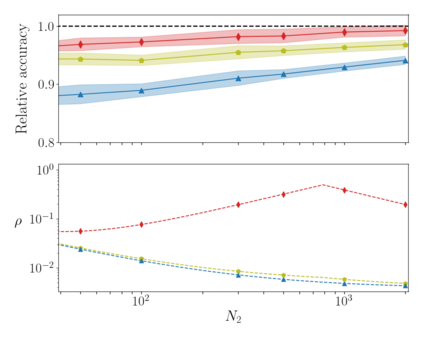
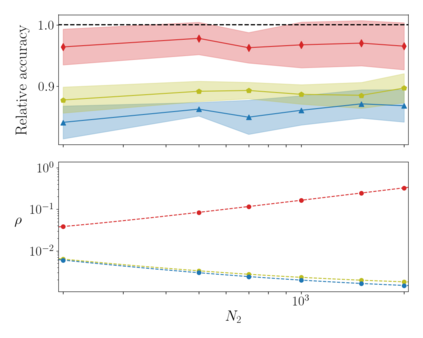
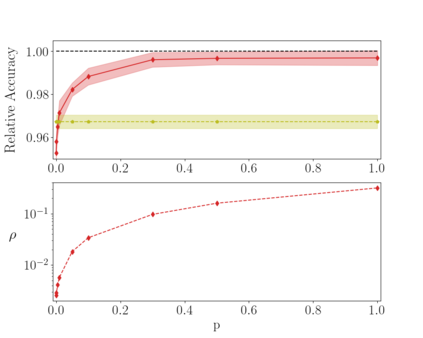
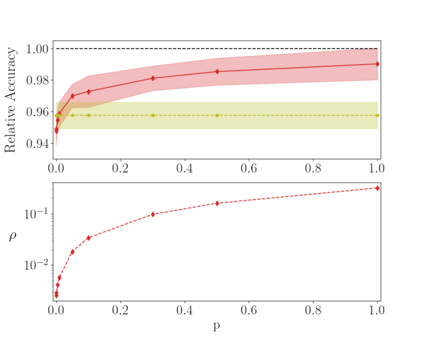
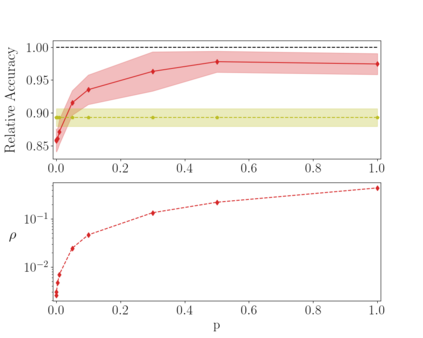
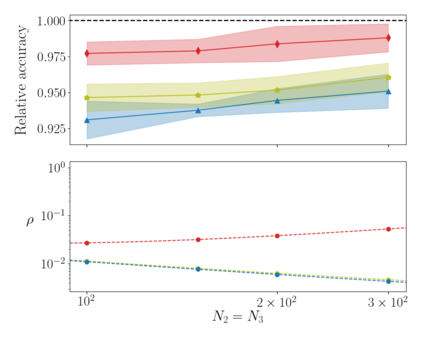
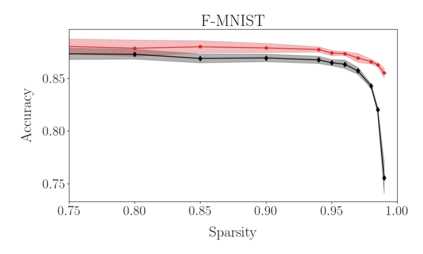
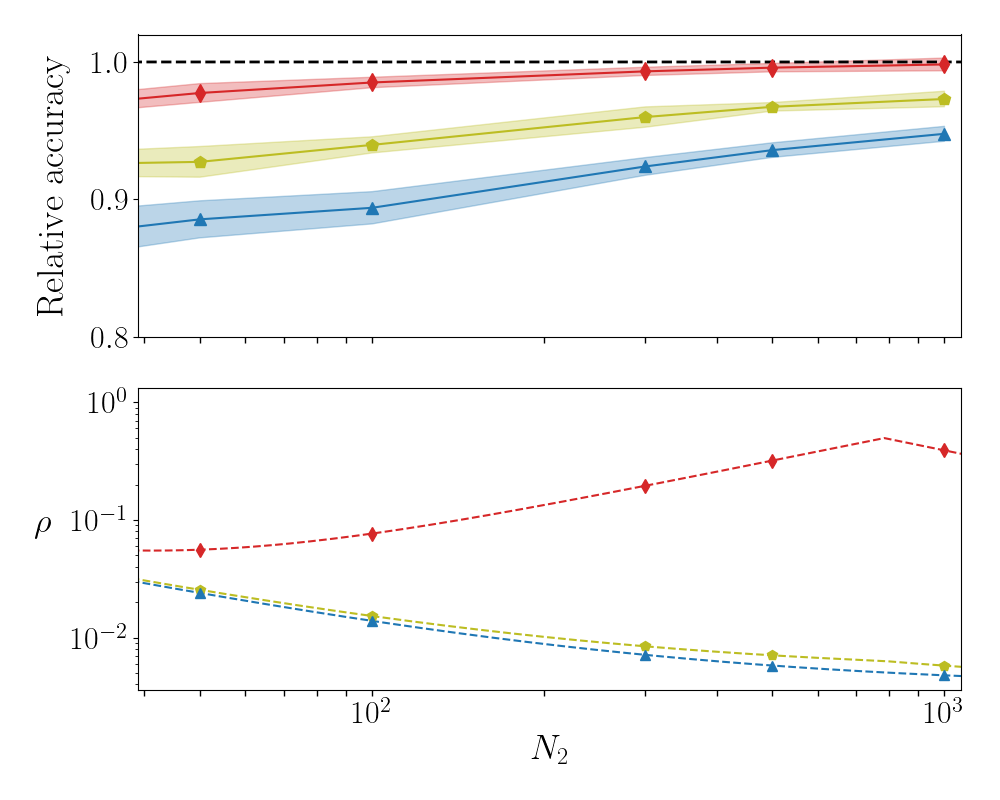
Deep neural networks can be trained in reciprocal space, by acting on the eigenvalues and eigenvectors of suitable transfer operators in direct space. Adjusting the eigenvalues, while freezing the eigenvectors, yields a substantial compression of the parameter space. This latter scales by definition with the number of computing neurons. The classification scores, as measured by the displayed accuracy, are however inferior to those attained when the learning is carried in direct space, for an identical architecture and by employing the full set of trainable parameters (with a quadratic dependence on the size of neighbor layers). In this Letter, we propose a variant of the spectral learning method as appeared in Giambagli et al {Nat. Comm.} 2021, which leverages on two sets of eigenvalues, for each mapping between adjacent layers. The eigenvalues act as veritable knobs which can be freely tuned so as to (i) enhance, or alternatively silence, the contribution of the input nodes, (ii) modulate the excitability of the receiving nodes with a mechanism which we interpret as the artificial analogue of the homeostatic plasticity. The number of trainable parameters is still a linear function of the network size, but the performances of the trained device gets much closer to those obtained via conventional algorithms, these latter requiring however a considerably heavier computational cost. The residual gap between conventional and spectral trainings can be eventually filled by employing a suitable decomposition for the non trivial block of the eigenvectors matrix. Each spectral parameter reflects back on the whole set of inter-nodes weights, an attribute which we shall effectively exploit to yield sparse networks with stunning classification abilities, as compared to their homologues trained with conventional means.
翻译:深神经网络可以在对等空间中接受培训, 方法是在直接空间使用合适的传输操作员的egen值和 eigenvalies 进行相应的调整。 调整 eigenvalies, 并冻结 eigenevors, 产生参数空间的大幅压缩 。 后一种根据计算神经元数定义的尺度。 以显示的准确度衡量的分类分数无论如何都不如在直接空间进行学习、 同一结构, 并使用全套可训练参数( 以邻接层大小为四级依赖值) 。 在此信件中, 我们建议使用 Giambagli 和 {Nat. Comm.} 2021 中出现的光谱参数学习方法的变异, 该变异种将利用两组的egen值, 用于相邻层之间的每次绘图。 egenvalual 值的作用是可自由调整的 knobs, 以便( i) 增强, 或者说, 使输入的直径直径直径直径直径直径直径的值值值值值值值值值值值值值值值值值值值值值值值值值值的值值值值值值值值值值, 。 (ii) 我们用接受的分解的分解的分解的分解的分解的分数, 。