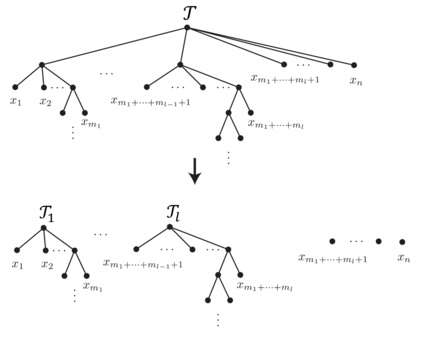
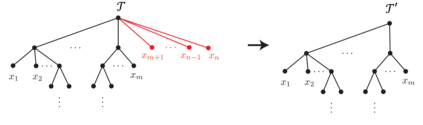
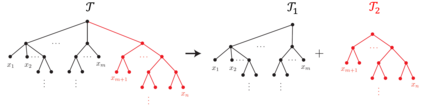
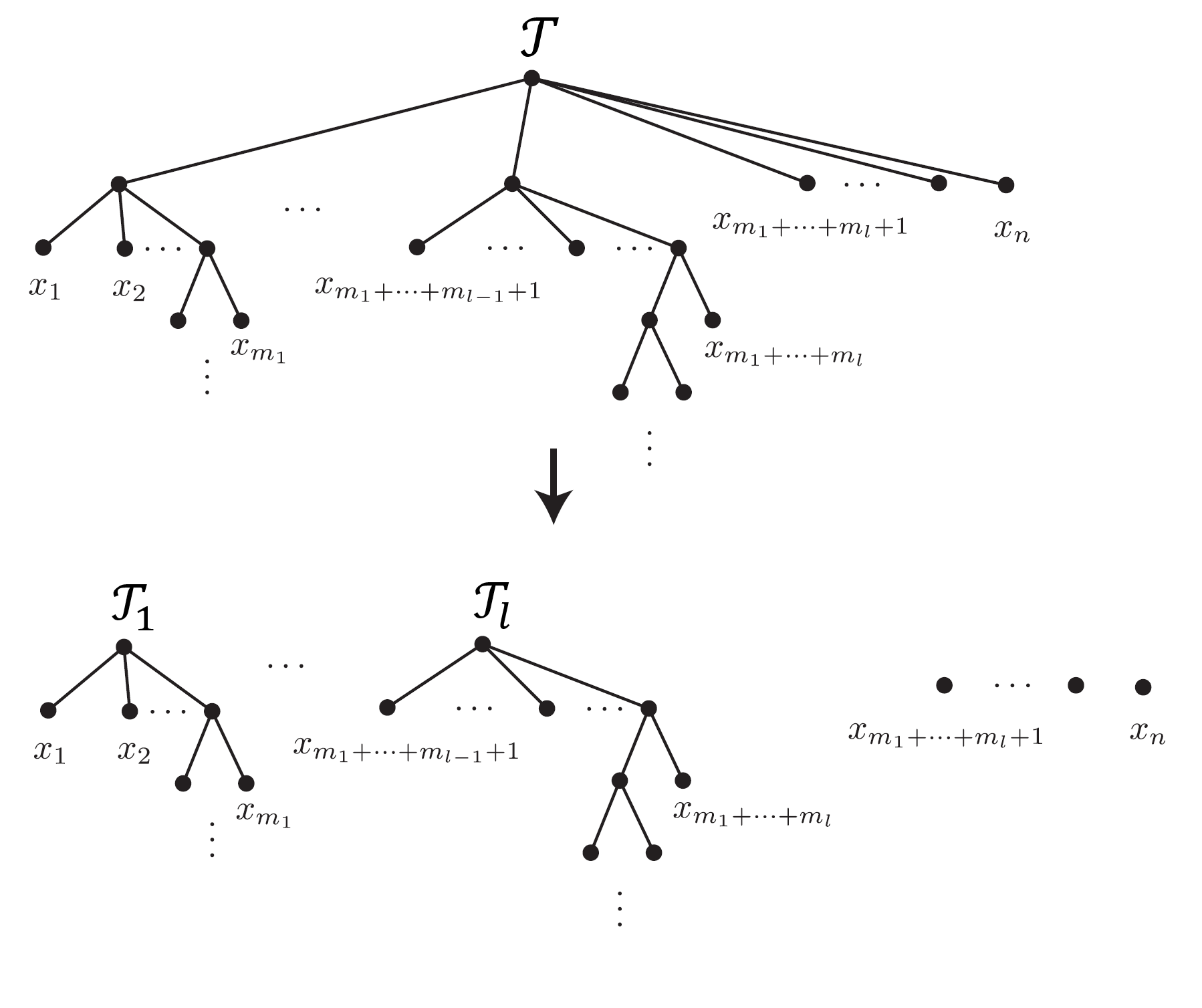
Neural networks are versatile tools for computation, having the ability to approximate a broad range of functions. An important problem in the theory of deep neural networks is expressivity; that is, we want to understand the functions that are computable by a given network. We study real infinitely differentiable (smooth) hierarchical functions implemented by feedforward neural networks via composing simpler functions in two cases: 1) each constituent function of the composition has fewer inputs than the resulting function; 2) constituent functions are in the more specific yet prevalent form of a non-linear univariate function (e.g. tanh) applied to a linear multivariate function. We establish that in each of these regimes there exist non-trivial algebraic partial differential equations (PDEs), which are satisfied by the computed functions. These PDEs are purely in terms of the partial derivatives and are dependent only on the topology of the network. For compositions of polynomial functions, the algebraic PDEs yield non-trivial equations (of degrees dependent only on the architecture) in the ambient polynomial space that are satisfied on the associated functional varieties. Conversely, we conjecture that such PDE constraints, once accompanied by appropriate non-singularity conditions and perhaps certain inequalities involving partial derivatives, guarantee that the smooth function under consideration can be represented by the network. The conjecture is verified in numerous examples including the case of tree architectures which are of neuroscientific interest. Our approach is a step toward formulating an algebraic description of functional spaces associated with specific neural networks, and may provide new, useful tools for constructing neural networks.
翻译:神经网络是多种计算功能的多功能工具。 深神经网络理论的一个重要问题是直线多变函数中应用的非线性单一空间功能( 如 tanh) 。 我们想要理解由特定网络可比较的函数。 我们研究由进化向神经网络通过设置更简单的函数而执行的无穷尽差异( mooth) 级功能。 在两种情况下, 我们研究进化向神经网络所执行的真正差异性( PDEs ) : 1) 组成结构的每个组成功能的输入量少于由此产生的功能; 2 组成功能是非线性单向空空空空空空间函数( 如 tanh) 的较具体形式( tanh) 。 我们确定, 在这些系统中,每个系统都存在非边际的平差部分等等方程式( PDEs ) 。 这些PDEs 纯粹是部分衍生工具, 仅取决于网络的表层层结构, 并且通过直线性结构的阶结构的阶梯度产生新的方形方形方形 。