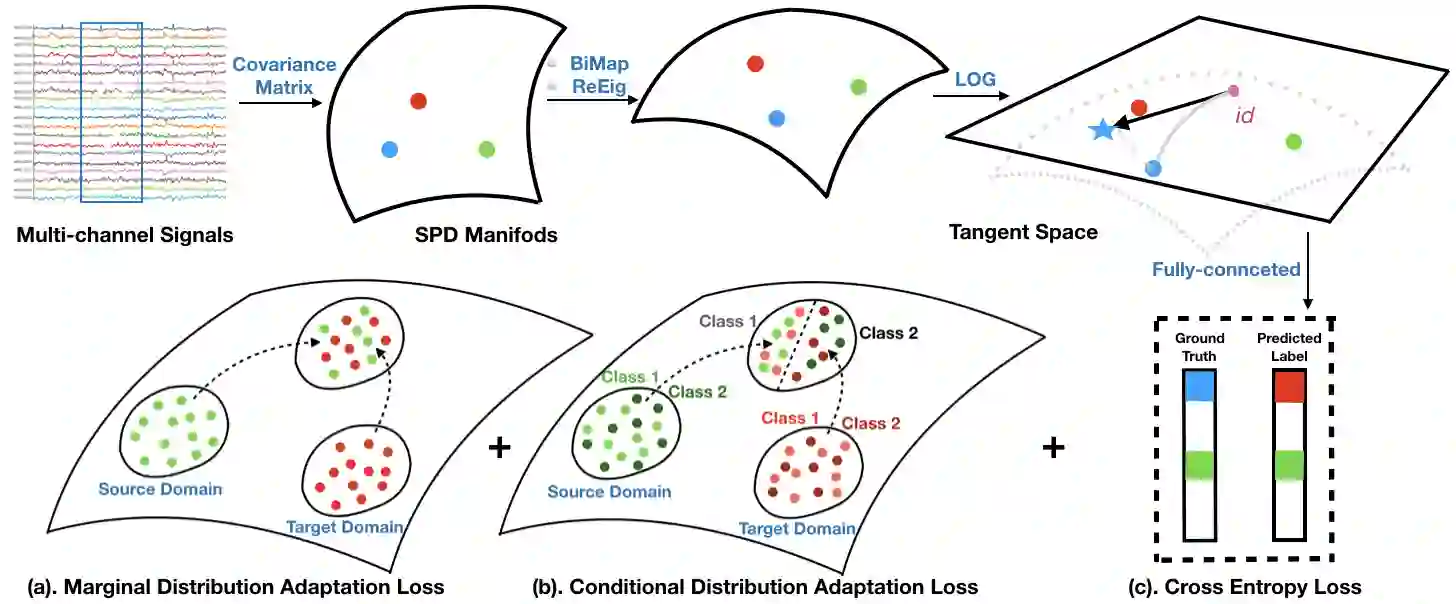
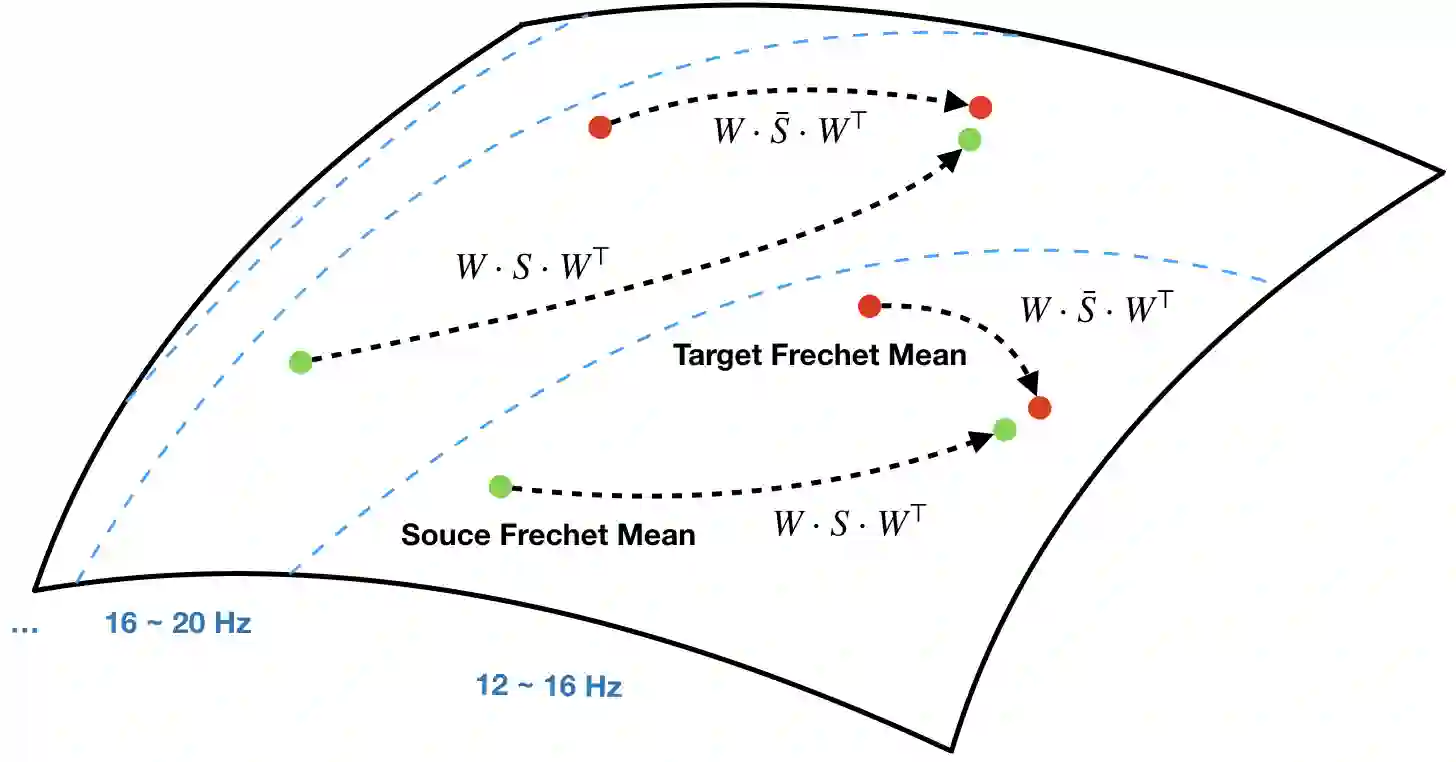
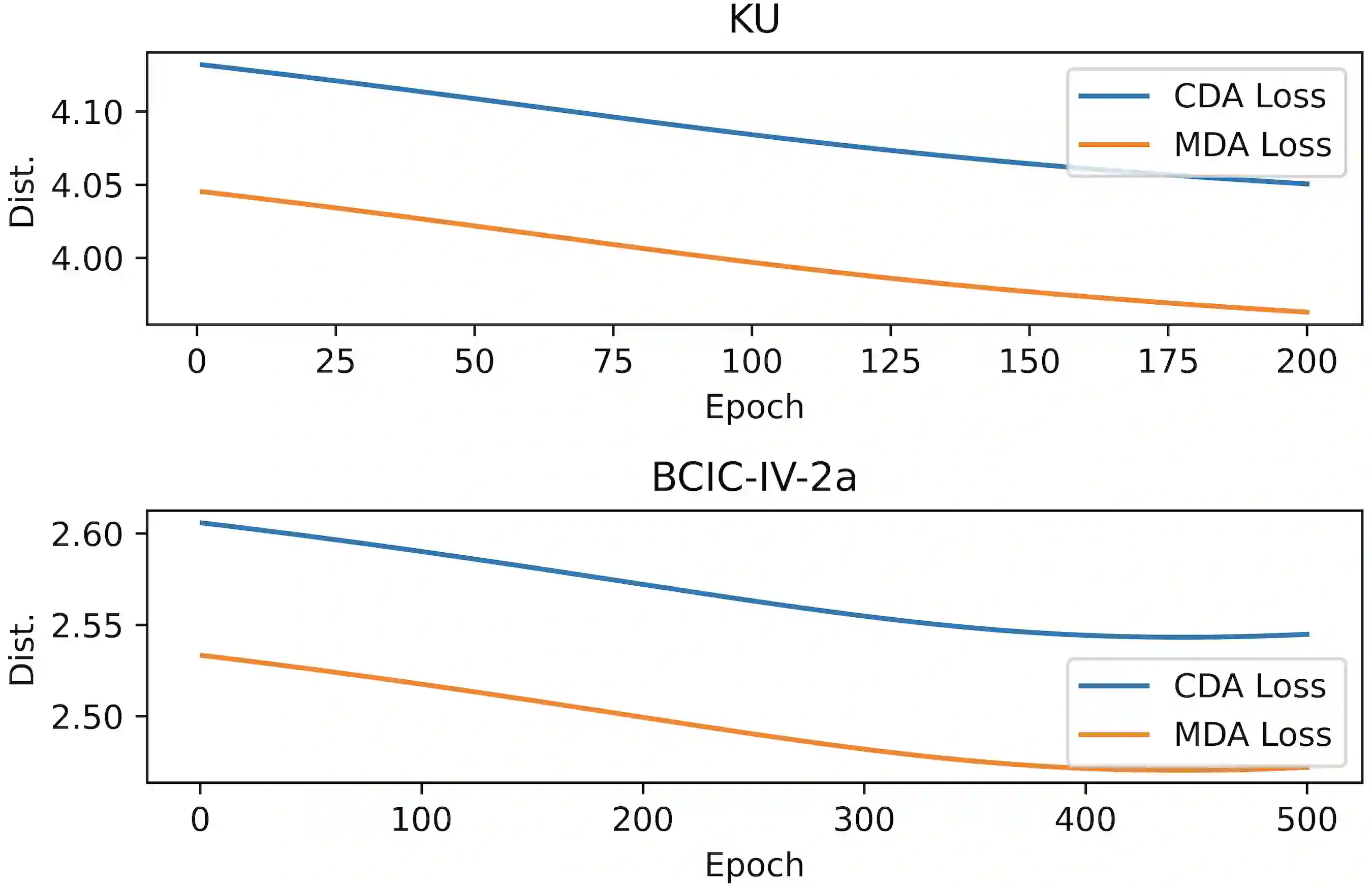
The domain adaptation (DA) problem on symmetric positive definite (SPD) manifolds has raised interest in the machine learning community because of the growing potential for the SPD-matrix representations across many cross-domain applicable scenarios. However, due to the different underlying space, the previous experience and solution to the DA problem cannot benefit this new scenario directly. This study addresses a specific DA problem: the marginal and conditional distributions differ in the source and target domains on SPD manifolds. We then formalize this problem from an optimal transport perspective and derive an optimal transport framework on SPD manifolds for supervised learning. In addition, we propose a computational scheme under the optimal transport framework, Deep Optimal Transport (DOT), for general computation, using the generalized joint distribution adaptation approach and the existing Riemannian-based network architectures on SPD manifolds. DOT is applied to the real-world scenario and becomes a specific EEG-BCI classifier against the cross-session motor-imagery classification from the calibration phase to the feedback phase. In the experiments, DOT exhibits a marked improvement in the average accuracy in two highly non-stationary cross-session scenarios in the EEG-BCI classification, respectively, indicating the proposed methodology's validity.
翻译:对正确定值(SPD)参数的域适应(DA)问题引起对机器学习界的兴趣,因为在许多跨领域适用的假设情景中,SPD-矩阵表示形式的潜力日益增大,但是,由于基础空间不同,以前的经验和DA问题的解决办法不能直接使这一新假设方案受益。本研究涉及一个具体的DA问题:SPD 元体的源和目标领域在源和目标领域存在不同的边际和有条件分布。然后,我们从最佳运输角度将这一问题正式确定下来,并在SPD 元数据上形成一个最佳运输框架,用于监督学习。此外,我们提议在最佳运输框架“深最佳运输”(DOT)下,采用通用联合分配适应办法和现有的Riemannian SPD 元件网络结构进行一般计算。DOT应用于现实世界情景,并成为从校准阶段到反馈阶段跨会期马达象图像分类的一个特定的EG-BCI分类。在实验中,DOT展示了两种高度非静止的跨层方法中的平均精确度,分别表明EG-I的拟议的E-EG-G-I跨级设想方案。