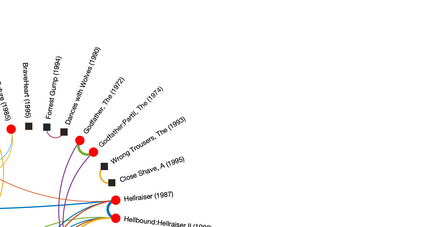
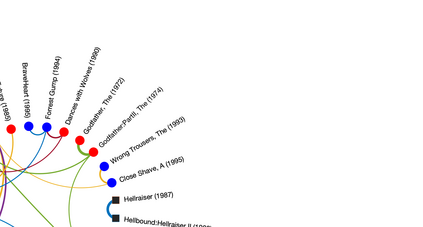
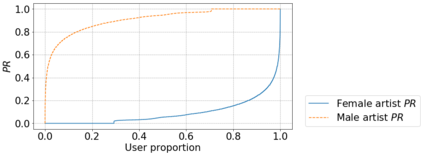
Inference of community structure in probabilistic graphical models may not be consistent with fairness constraints when nodes have demographic attributes. Certain demographics may be over-represented in some detected communities and under-represented in others. This paper defines a novel $\ell_1$-regularized pseudo-likelihood approach for fair graphical model selection. In particular, we assume there is some community or clustering structure in the true underlying graph, and we seek to learn a sparse undirected graph and its communities from the data such that demographic groups are fairly represented within the communities. Our optimization approach uses the demographic parity definition of fairness, but the framework is easily extended to other definitions of fairness. We establish statistical consistency of the proposed method for both a Gaussian graphical model and an Ising model for, respectively, continuous and binary data, proving that our method can recover the graphs and their fair communities with high probability.
翻译:在概率图形模型中,社区结构的推论可能不符合在节点具有人口属性时的公平性限制。某些人口统计在一些被检测到的社区中可能代表过多,而在另一些社区中则代表不足。本文定义了用于公平图形模型选择的新颖的1美元1美元的正规化假象方法。特别是,我们假定在真实的基本图中存在某种社区或群集结构,我们试图从数据中学习一个稀少的无方向的图表及其社区,从而让人口群体在社区中得到公平的代表。我们优化方法使用了公平的人口均等定义,但框架很容易扩展到其他公平定义。我们为高斯图形模型和连续和二进制数据分别确定了拟议方法的统计一致性,证明我们的方法可以极有可能恢复这些图表及其公平的社区。