Order-based Structure Learning without Score Equivalence

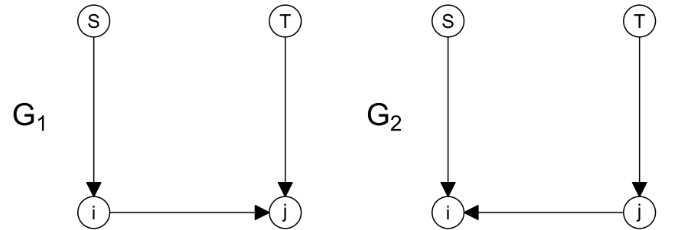
We consider the structure learning problem with all node variables having the same error variance, an assumption known to ensure the identifiability of the causal directed acyclic graph (DAG). We propose an empirical Bayes formulation of the problem that yields a non-decomposable posterior score for DAG models. To facilitate efficient posterior computation, we approximate the posterior probability of each ordering by that of a "best" DAG model, which naturally leads to an order-based Markov chain Monte Carlo (MCMC) algorithm. Strong selection consistency for our model is proved under mild high-dimensional conditions, and the mixing behavior of our sampler is theoretically investigated. Further, we propose a new iterative top-down algorithm, which quickly yields an approximate solution to the structure learning problem and can be used to initialize the MCMC sampler. We demonstrate that our method outperforms other state-of-the-art algorithms under various simulation settings, and conclude the paper with a single-cell real-data study illustrating practical advantages of the proposed method.