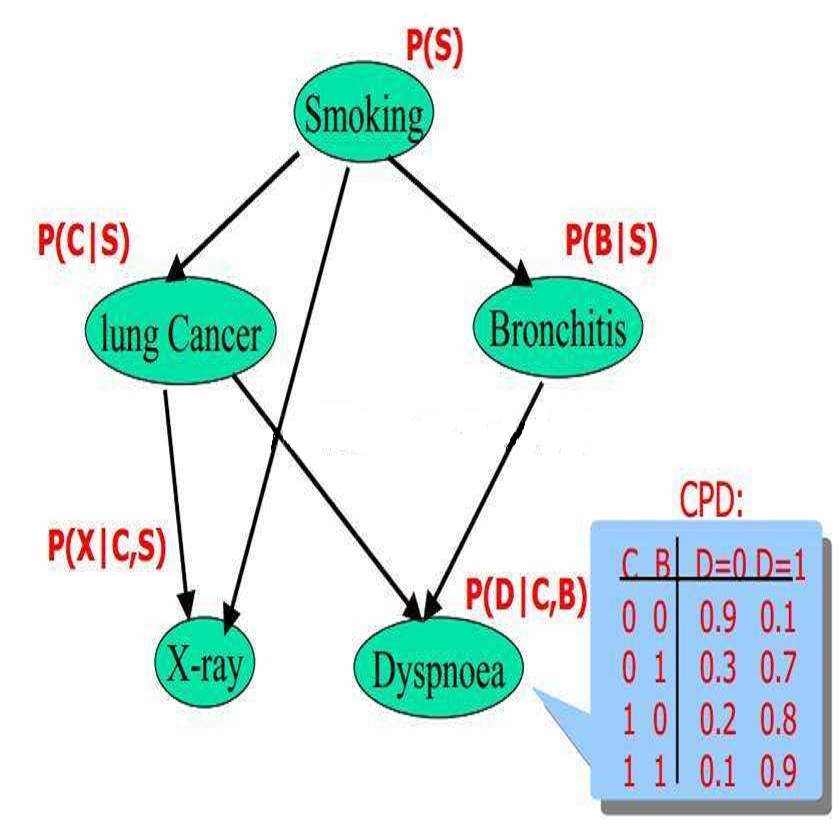
This paper considers the problem of testing the maximum in-degree of the Bayes net underlying an unknown probability distribution $P$ over $\{0,1\}^n$, given sample access to $P$. We show that the sample complexity of the problem is $\tilde{\Theta}(2^{n/2}/\varepsilon^2)$. Our algorithm relies on a testing-by-learning framework, previously used to obtain sample-optimal testers; in order to apply this framework, we develop new algorithms for ``near-proper'' learning of Bayes nets, and high-probability learning under $\chi^2$ divergence, which are of independent interest.
翻译:本文考虑了在给定对P的样本访问的情况下,测试未知概率分布P上的贝叶斯网络最大入度的问题。我们证明了该问题的样本复杂度为$ \tilde {\Theta}(2^{n/2}/\varepsilon^2) $。我们的算法依赖于“测试-学习”框架,该框架先前已用于获得样本最优测试器;为了应用该框架,我们开发了新的算法,用于“近似正确”地学习贝叶斯网络,并在卡方散度下进行高概率学习,这些算法的独立兴趣。