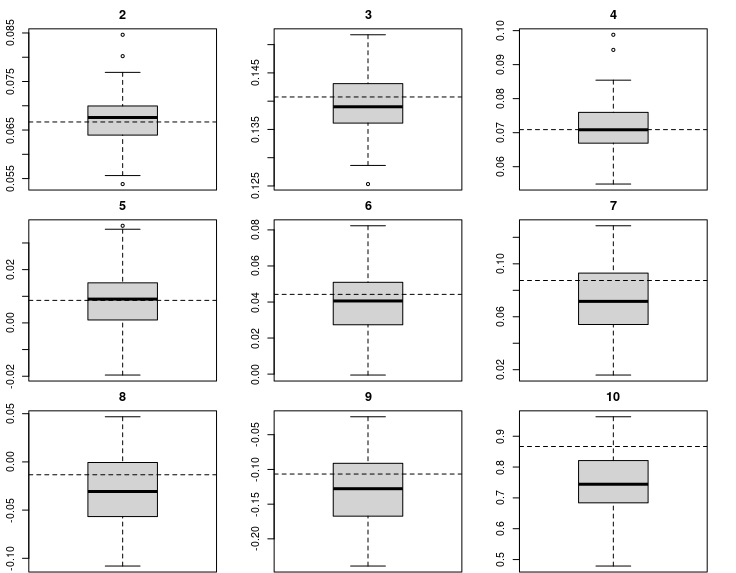
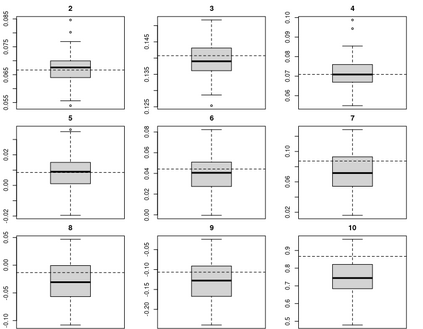
Copulas are a powerful tool to model dependence between the components of a random vector. One well-known class of copulas when working in two dimensions is the Farlie-GumbelMorgenstern (FGM) copula since their simple analytic shape enables closed-form solutions to many problems in applied probability. However, the classical definition of high-dimensional FGM copula does not enable a straightforward understanding of the effect of the copula parameters on the dependence, nor a geometric understanding of their admissible range. We circumvent this issue by studying the FGM copula from a probabilistic approach based on multivariate Bernoulli distributions. This paper studies high-dimensional exchangeable FGM copulas, a subclass of FGM copulas. We show that dependence parameters of exchangeable FGM can be expressed as convex hulls of a finite number of extreme points and establish partial orders for different exchangeable FGM copulas (including maximal and minimal dependence). We also leverage the probabilistic interpretation to develop efficient sampling and estimating procedures and provide a simulation study. Throughout, we discover geometric interpretations of the copula parameters that assist one in decoding the dependence of high-dimensional exchangeable FGM copulas.
翻译:Copula 是一种强大的工具,可以模拟随机矢量各组成部分之间的依赖性。在两个层面开展工作时,众所周知的一流的相生体是Farlie-GumbelMorgenstern (FGM) 相生体,因为其简单的分析形状能够以封闭的形式解决应用概率方面的许多问题。然而,高度女性生殖器残割的典型定义并不能直接理解阴极参数对依赖性的影响,也无法对其可允许范围进行几何理解。我们通过研究基于多变伯努利分布的概率方法来规避这一问题。本文研究高维可交换的女生殖器残割合质,这是女性生殖器残割的子类。我们表明,可交换的女性生殖器的依赖性参数可以表现为数量有限的极端点的共生体,为不同可交换的可交换女性生殖器残割椰子(包括最大和最低依赖性)的部分命令。我们还利用概率解释来制定高效的取样和估计程序,并提供模拟研究。我们从总体上发现了可解释的可变性参数的几何解释性解释,有助于进行高度的切分解。