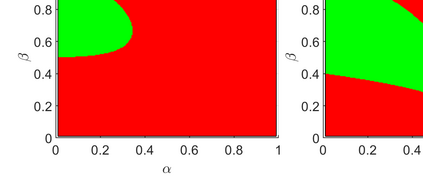
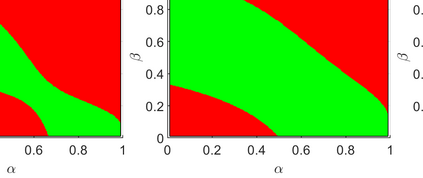
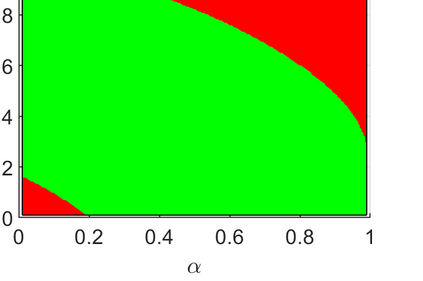
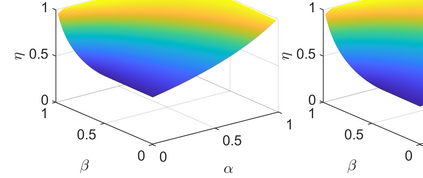
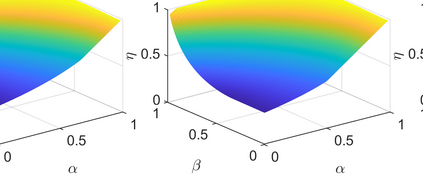
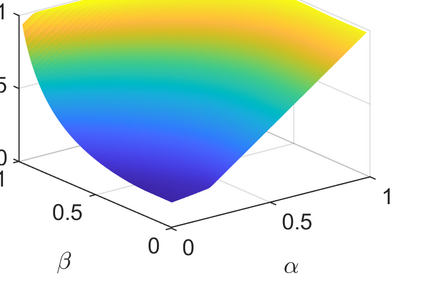
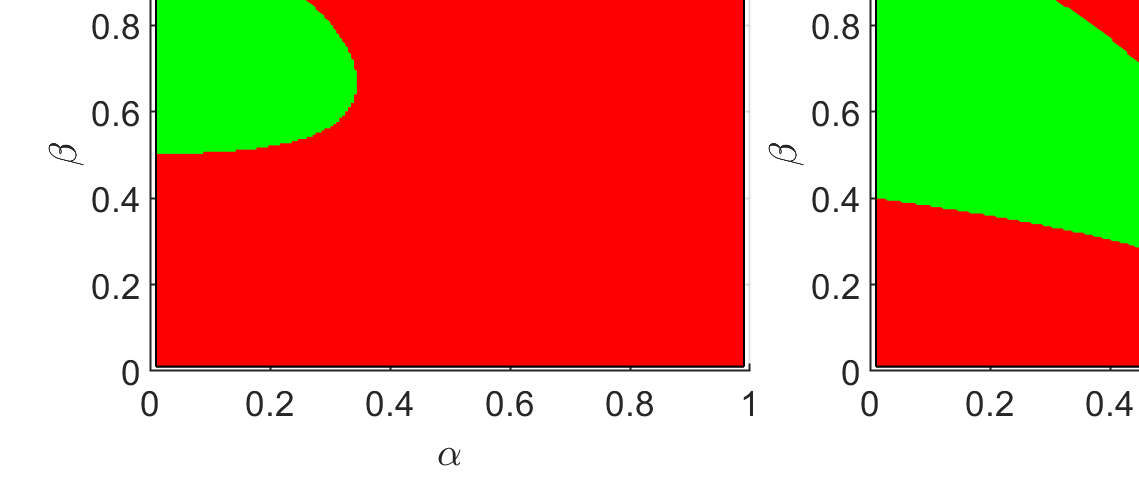
Conditionally specified models are often used to describe complex multivariate data. Such models assume implicit structures on the extremes. So far, no methodology exists for calculating extremal characteristics of conditional models since the copula and marginals are not expressed in closed forms. We consider bivariate conditional models that specify the distribution of $X$ and the distribution of $Y$ conditional on $X$. We provide tools to quantify implicit assumptions on the extremes of this class of models. In particular, these tools allow us to approximate the distribution of the tail of $Y$ and the coefficient of asymptotic independence $\eta$ in closed forms. We apply these methods to a widely used conditional model for wave height and wave period. Moreover, we introduce a new condition on the parameter space for the conditional extremes model of Heffernan and Tawn (2004), and prove that the conditional extremes model does not capture $\eta$, when $\eta<1$.
翻译:有条件指定的模型通常用于描述复杂的多变数据。 这些模型假定极端的隐含结构。 到目前为止,目前还没有计算有条件模型极端特征的方法,因为没有以封闭形式表示相交和边际。 我们考虑双变有条件模型,具体规定X美元的分布和以X美元为条件的Y美元分布。 我们提供了工具,以量化关于这一类模型极端的隐含假设。 特别是,这些工具使我们能够以封闭形式估计Y$的尾巴分布和无线独立系数$\eta$。 我们将这些方法应用于广泛使用的波高和波期有条件模型。 此外,我们还对赫弗南和陶恩的有条件极端模型的参数空间引入了新的条件 (2004年), 并证明条件极端模型在 $<1美元时并不包含$\eta$ 。