On Local Convergence of Iterative Hard Thresholding for Matrix Completion

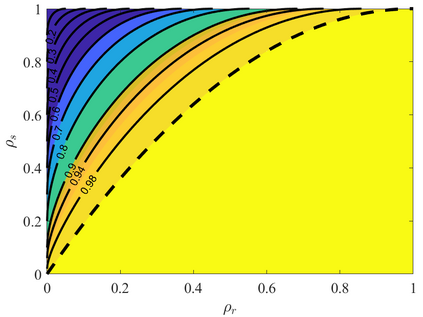
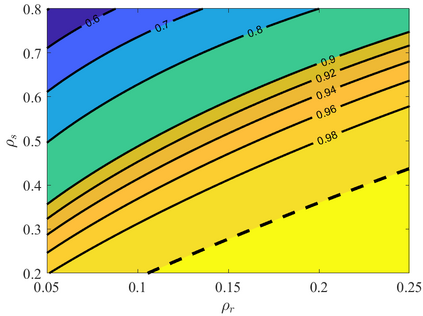
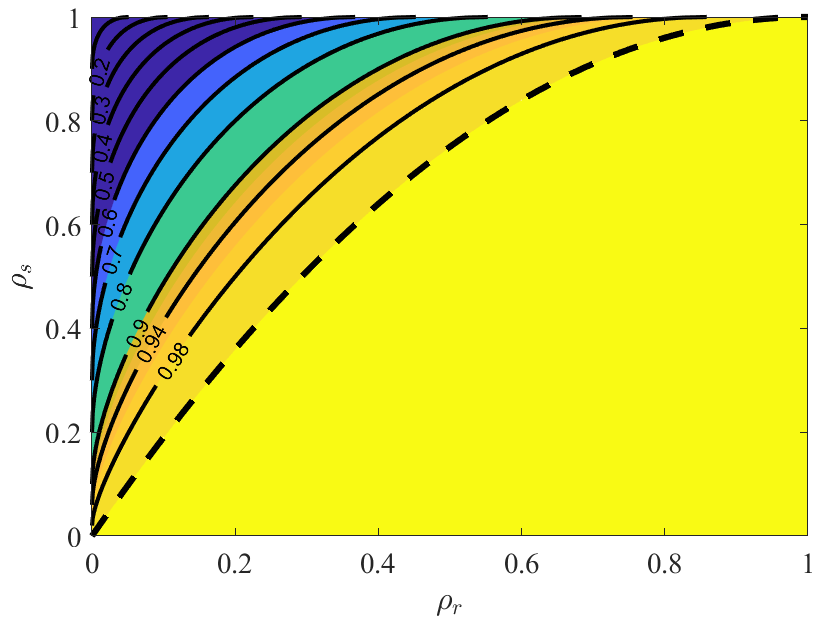
Iterative hard thresholding (IHT) has gained in popularity over the past decades in large-scale optimization. However, convergence properties of this method have only been explored recently in non-convex settings. In matrix completion, existing works often focus on the guarantee of global convergence of IHT via standard assumptions such as incoherence property and uniform sampling. While such analysis provides a global upper bound on the linear convergence rate, it does not describe the actual performance of IHT in practice. In this paper, we provide a novel insight into the local convergence of a specific variant of IHT for matrix completion. We uncover the exact linear rate of IHT in a closed-form expression and identify the region of convergence in which the algorithm is guaranteed to converge. Furthermore, we utilize random matrix theory to study the linear rate of convergence of IHTSVD for large-scale matrix completion. We find that asymptotically, the rate can be expressed in closed form in terms of the relative rank and the sampling rate. Finally, we present various numerical results to verify the aforementioned theoretical analysis.