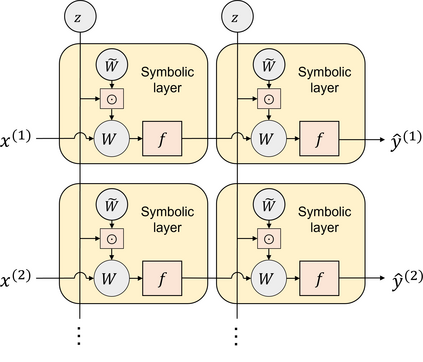
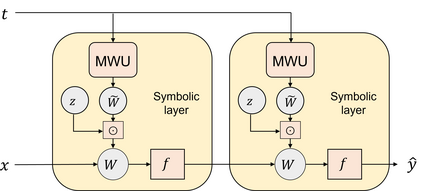
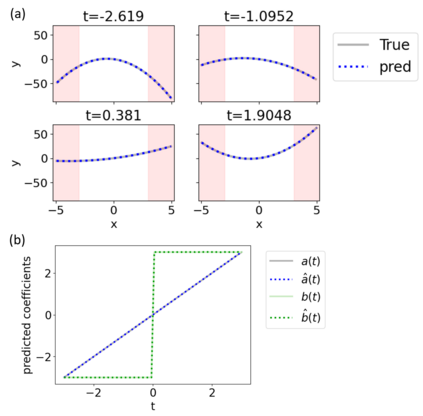
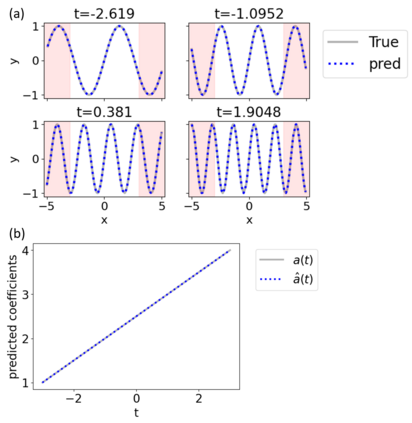
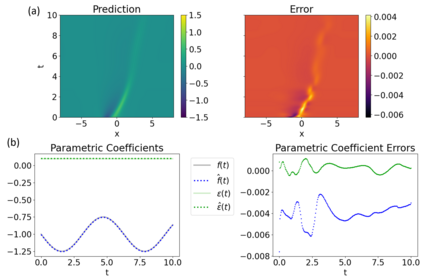
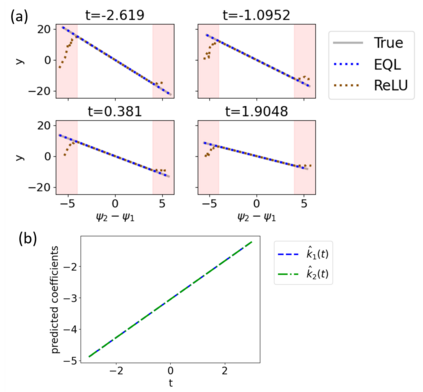
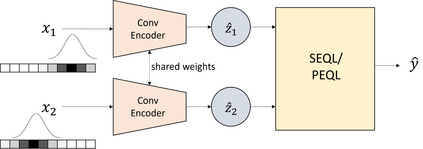
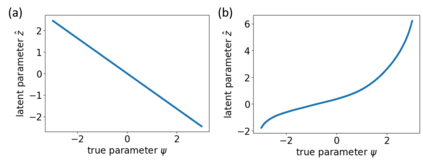
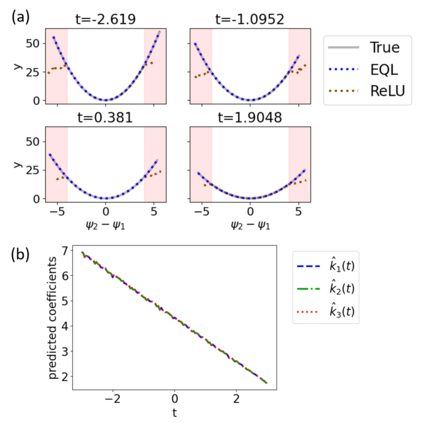
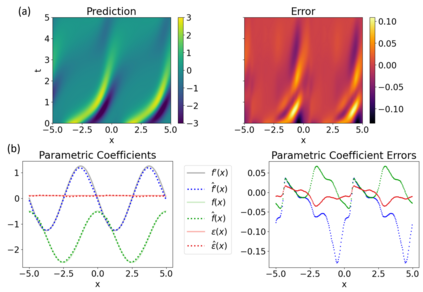
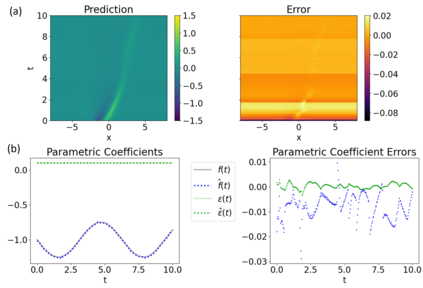
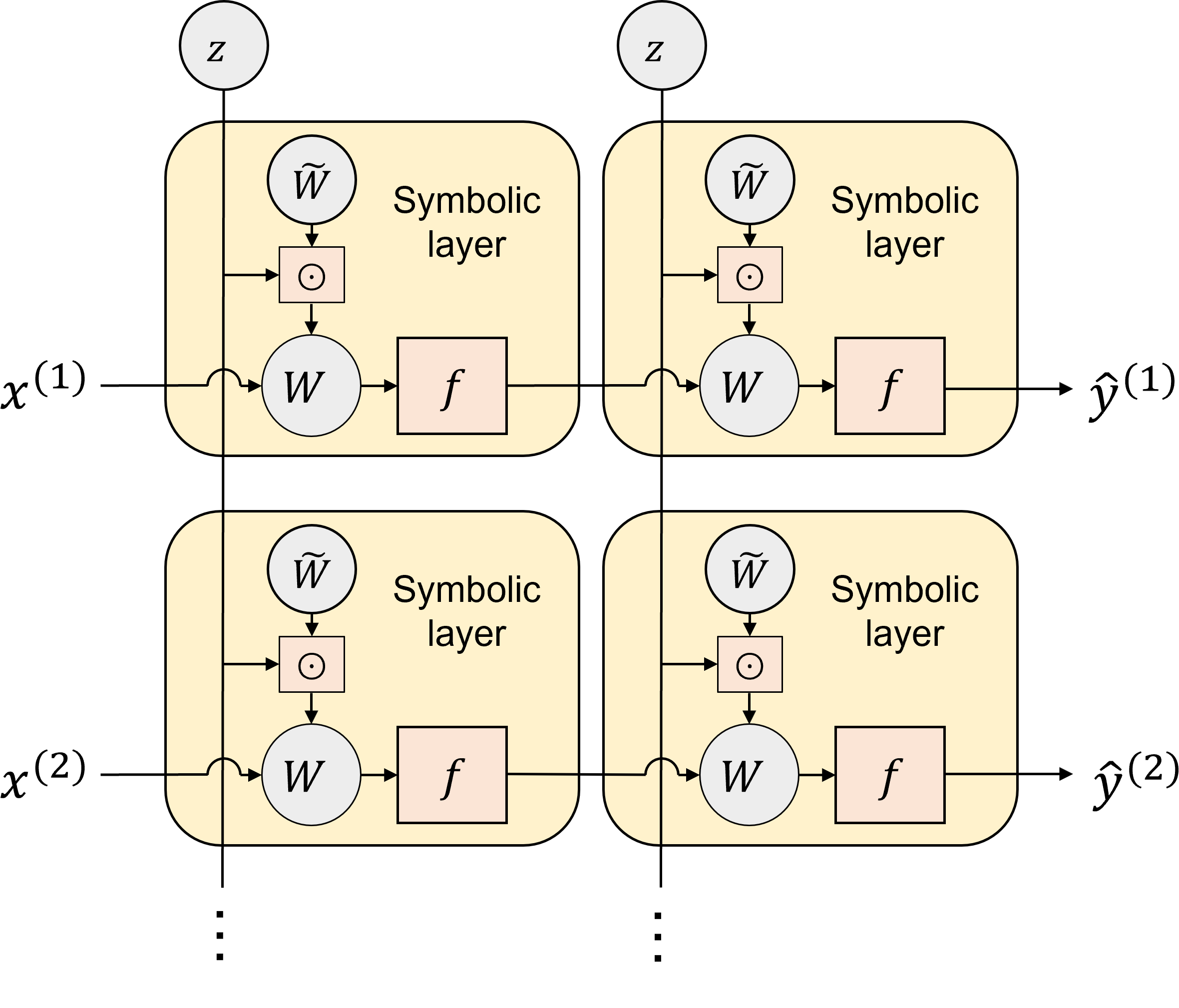
Symbolic regression is a machine learning technique that can learn the governing formulas of data and thus has the potential to transform scientific discovery. However, symbolic regression is still limited in the complexity and dimensionality of the systems that it can analyze. Deep learning on the other hand has transformed machine learning in its ability to analyze extremely complex and high-dimensional datasets. We propose a neural network architecture to extend symbolic regression to parametric systems where some coefficient may vary but the structure of the underlying governing equation remains constant. We demonstrate our method on various analytic expressions, ODEs, and PDEs with varying coefficients and show that it extrapolates well outside of the training domain. The neural network-based architecture can also integrate with other deep learning architectures so that it can analyze high-dimensional data while being trained end-to-end. To this end we integrate our architecture with convolutional neural networks to analyze 1D images of varying spring systems.
翻译:符号回归是一种机器学习技术,可以学习数据治理公式,从而有可能改变科学发现。然而,象征性回归在它所能分析的系统的复杂性和维度方面仍然有限。另一方面,深层次学习改变了机器分析极其复杂和高维数据集的能力。我们提议一个神经网络结构,将象征性回归扩展至参数系统,其中某些系数可能不同,但基本治理方程的结构保持不变。我们用各种分析表达、ODE和PDE展示了我们的方法,其系数各不相同,并表明它极有可能在培训领域之外外进行外推。基于神经网络的建筑还可以与其他深层学习结构相结合,以便它能够分析高维数据,同时接受终端到终端培训。为此,我们将我们的架构与革命神经网络结合起来,以分析不同春季系统的1D图像。